ANÁLISIS GEOESPACIAL DEL ÍNDICE DE ADSORCIÓN (Kd) DE ATRAZINA CALCULADO SEGÚN CARTAS DE SUELOS Y MUESTREO EN GRILLA

MIGUEL ALEJANDRO BECERRA¹*; SUSANA HANG² & MARTÍN DÍAZ-ZORITA³

1 CONICET.
2 Facultad de Ciencias Agropecuarias, Universidad Nacional de Córdoba.
3 CONICET (INBA) y Novozymes Bioag S.A.

* Autor de contacto: mabecerra@agro.unc.edu.ar

Recibido: 19-11-14
Recibido con revisiones: 03-08-15
Aceptado: 03-08-15

RESUMEN

Las cartas de suelos reúnen abundante información, a veces subutilizada, de propiedades edáficas, distribución y variabilidad de los suelos a escala regional. Mediante funciones de edafotransferencia es posible generar información sobre nuevos atributos. El propósito de este estudio fue caracterizar la variación espacial del índice de retención, K_d, de atrazina (6-Cloro-N2-etil-N4-isopropil-1,3,5-triazina-2,4-diamina) calculado a partir de dos fuentes de datos: un muestreo reciente (Kd_m) y las cartas de suelo (Kd estimado) y evaluar el desempeño de diferentes métodos de utilización de los datos de las cartas de suelos para su estimación. Para los Kd estimados se evaluaron cinco métodos de obtención: uno con los datos analíticos de la serie predominante de la unidad cartográfica, otro tomando un promedio ponderado en base a la participación de las series en la unidad cartográfica y los restantes según tres criterios de interpolación. Se trabajó en dos sistemas hidrológicos con características edáficas contrastantes: Morteros (SHM) y Río Quinto (SHRQ). Los Kd_m de SHM se distribuyeron desde bajos a altos con un promedio de 2,03 ± 0,87 L kg^-1; mientras que en el SHRQ los Kd se concentraron en valores bajos con un promedio de 0,79 ± 0,71 L kg^-1. El análisis de regresión lineal entre los Kd_m y los Kd estimados mostró mejor ajuste para el caso de las interpolaciones con respecto a los provenientes de las cartas. Los menores errores de estimación (<1 L kg^-1) correspondieron al rango de Kd entre 0,06 y 2,84 L kg^-1. Los errores mayores (>1 L kg^-1) fueron menos frecuentes para las interpolaciones que para los mapas de unidades cartográficas, y representaron un promedio de casos de 20,6% y 34,1%, respectivamente. Este trabajo mostró que la información de las cartas de suelos, para los atributos evaluados, no es sustancialmente diferente a la obtenida por un muestreo actual.

Palabras clave. Variabilidad espacial, criterios de interpolación, SIG, riesgo ambiental.

GEOSPATIAL ANALYSIS OF ATRAZINE ADSORPTION INDEX (Kd) AS CALCULATED BY SOIL MAPS AND GRID SAMPLING

ABSTRACT

Soil surveys provide information, sometimes under-used, about distribution and variability of soil characteristics at a regional scale. Pedotransfer functions generate information on new soil attributes. The purpose of this study was to characterize the spatial variability of the atrazine (6-chloro-N2-ethyl-N4-isopropyl-1,3,5-triazine-2,4-diamine) retention index, Kd, calculated from two data sources: soil surveys (estimated Kd) and a recent regional soil sampling (Kd_m); and to assess different methods to estimate Kd at the regional scale from soil surveys data. To obtain the estimated Kd, five methods were assessed: one using the data of the predominant soil series of the cartographic unit, another using the weighted arithmetic mean of the data of the soil series within the cartographic unit, and the remaining three from different interpolation methods. Two hydrological units with contrasting soil characteristics were studied: Morteros (SHM) and Río Quinto (SHRQ). Kd_m corresponding to SHM oscillated from low to high with an average of 2.03 ± 0.87 L kg^-1 while Kd_m values of the SHRQ were mostly low, with an average of 0.79 ± 0.71 L kg^-1. Linear regression analysis between Kd_m and the estimated Kds fitted better with the interpolated Kds than with the soil surveys Kds. Lower estimation errors (< 1 L kg^-1) corresponded with the Kd_m range between 0.06 and 2.84 L kg^-1. Higher estimation errors (> 1 L kg^-1) were less common for the interpolations than for cartographic unit maps, representing 20.6% and 34.1% of the cases, respectively. This study showed that the information from soil surveys was consistent with the data obtained from a recent sampling.

Key words. Spatial variability, interpolation criteria, GIS, environmental risk.

INTRODUCCIÓN

La cartografía de suelos ha contribuido al conocimiento, localización, distribución y planificación del aprovechamiento de los recursos agropecuarios de una manera objetiva, práctica y sencilla (López et al., 1981). Las cartas de suelos constituyen un valioso inventario de los diferentes tipos de suelo, su extensión y distribución espacial, por lo que pueden utilizarse para hacer predicciones acerca de las cualidades y potencialidades de esos suelos (Manchanda et al., 2002). Mediante el uso de funciones de edafotrans-ferencia estas cualidades pueden ser derivadas a partir de las características descriptas en las cartas para esos suelos (Wagenet et al., 1991). Sin embargo, los estudios regionales que utilicen la información de las cartas de suelos enfrentan la limitante de la incertidumbre con respecto a la certeza de los datos publicados (Sonneveld et al., 2002). La vigencia de la información de las cartas de suelo ha sido motivo de diversos estudios. A modo de ejemplo, la disminución del contenido de carbono orgánico (CO) es un rasgo recurrente señalado para cartas de suelos de Gales e Inglaterra (Bellamy et al., 2005), en lugar de; Nueva Zelanda (Schipper et al., 2007) y Bélgica (Stevens & van Wesemael, 2008); para suelos de la región pampeana argentina, Berhongaray et al. (2013) reportaron una disminución del contenido de CO desde la introducción de la agricultura, aunque tal disminución sería previa a la época de confección de las cartas de suelos, no ocurriendo mayores cambios desde ese momento hasta la actualidad.

Los sistemas de información geográfica (SIG) en aplicaciones agrícolas constituyen una herramienta útil en la toma de decisiones (Petersen et al., 1995). Uno de los aspectos de mayor utilidad ha sido el estudio de la variabilidad espacial de suelos y la predicción de valores de atributos en sitios no muestreados a través del uso de las interpolaciones (Henríquez et al., 2005). Cuando se conoce el tipo de suelo de un sitio y es necesario estimar una propiedad, frecuentemente se recurre a utilizar el valor típico o un valor promedio para ese tipo de suelo. Sin embargo, ese enfoque presenta dos falencias; la primera es que no considera la variabilidad espacial del atributo dentro de cada tipo de suelo, y la segunda se refiere al cambio abrupto de los atributos entre un determinado tipo de suelo y el vecino. Este problema puede, en ocasiones, ser reducido a través del uso de métodos geoestadísticos como el kriging que considera la correlación espacial entre observaciones dentro y entre tipos de suelos (Goovaerts &Journel, 1995).

Cuantificar la retención de agroquímicos en el suelo es fundamental para entender y predecir su destino y transporte en el ambiente (Jayasundera et al., 2000). La retención se parametriza mediante índices tales como el Kd que relaciona la concentración del agroquímico entre la fase sólida y la solución. Sin embargo, una limitación es el uso de un mismo valor de Kd y su extrapolación a áreas extensas (Elabd et al., 1986). Dado que el Kd depende de las características de la molécula y de los atributos de suelo debiera ser considerado igual que cualquier otro parámetro del suelo sujeto a variación espacial, y por lo tanto, apto para cualquier metodología dedicada al análisis espacial.

La evaluación cuantitativa de la variabilidad espacial de los Kd es necesaria dado que las salidas de los modelos de simulación de destino de agroquímicos son muy sensibles al valor de entrada del índice de adsorción (Coquet & Ba-rriuso, 2002). No obstante, estas evaluaciones cuantitativas parecen ser escasas dado que la mayoría de los estudios de modelación estocástica que evalúan la variabilidad de la adsorción se apoyan en datos espaciales de contenido de CO en lugar de datos de Kd (Coquet & Barriuso, 2002).

Este trabajo tuvo dos objetivos. El primero fue evaluar la variación espacial del Kd de atrazina (6-Cloro-N2-etil-N4-isopropil-1,3,5-triazina-2,4-diamina), tomado como herbicida indicador, calculado a partir de dos fuentes de información: cartas de suelos y un muestreo regional reciente. El segundo objetivo fue valorar la precisión de métodos para la estimación de Kd a escala regional a partir de la información de las cartas de suelo.

MATERIALES Y MÉTODOS

Se recopiló la información del horizonte superficial de los suelos de la provincia de Córdoba a partir de las cartas de suelos (escala 1:100.000 y 1:50.000) y del mapa digital de suelos (escala 1:500.000) provisto por GeoINTA (2012). Se registraron los valores de materia orgánica del suelo (MOS), arcilla (ARC) y pH (relación suelo:agua 1:2,5) del perfil modal de cada serie. Como mapa base se utilizó el mapa de unidades cartográficas (UC) 1:500.000 debido a que no existen mapas de suelo a escala de mayor detalle para la totalidad de la provincia.

Entre 2012 y 2014 se llevó a cabo un muestreo en grilla de 20 km x 20 km, adaptada según la accesibilidad a los puntos de muestreo, georeferenciando cada punto con GPS. El mues-treo se realizó en dos regiones de características edáficas contrastantes, una correspondiente al sistema hidrológico Morteros (SHM) y la otra al sistema hidrológico del Río Quinto (SHRQ) (Fig. 1a).

Figura 1. a) Puntos de muestreo correspondientes a las áreas de los sistemas hidrológicos de Morteros (SHM) [cruces] y Río Quinto (SHRQ) [círculos]. b) Unidades cartográficas (UC) de la provincia de Córdoba a escala 1:500.000. Los puntos representan el centroide del polígono de cada UC.
Figure 1. a) Sampling points corresponding to Morteros hydrological unit (SHM) [crosses] and Río Quinto hydrological unit (SHRQ) [circles]. b) Cartographic units (CU) of the province of Córdoba in scale 1:500,000. Points represent the centroid of the polygon of each CU.

La zona correspondiente al SHM tiene su límite Oeste en la zona de sierras con altitud de hasta 2500 m snm, presentando una zona de llanura hacia el Este con altitud mínima de 59 m snm. En la región llana el clima es subhúmedo-húmedo a sub-húmedo-seco, con precipitaciones decrecientes de este a oeste de 900 a 500 mm anuales (SsRH, 2011). El SHRQ es de carácter interprovincial y pertenece al Sistema Pampeano. La altitud varía entre 1300 m snm al NO y100 m snm al E. Las precipitaciones disminuyen de noreste a sudoeste, entre los 600 y los 800 mm (SsRH, 2011). En el SHM los Molisoles ocupan el 64% del área, seguido por los Entisoles (19%) y los Alfisoles (17%). Por Gran Grupo dominan los Haplustoles (39%), seguido por Natra-cualfes (17%), Ustorthentes (17%), Argiudoles (7%) y Argius-toles (7%). En el SHRQ los Molisoles son los suelos predominantes (74,1%) seguido por los Entisoles (18,8) y los Alfisoles (7,1%). A nivel de Gran Grupo, los Haplustoles ocupan el 55,5%, secundados por Ustipsammentes (12,5%), Hapludoles (9,3%), Natralboles (7,0%) y Ustorthentes (6,1%).

En cada sitio se tomó una muestra de suelo de 0 a 15 cm de profundidad compuesta por 20 submuestras en un radio de 100 m alrededor del punto georeferenciado. Las muestras fueron secadas al aire, molidas y pasadas por tamiz de 2 mm. Se caracterizaron por CO por digestión húmeda con K₂Cr₂O₇ 1N (Walkley & Black) convertido en valores de materia orgánica (MOS) multiplicando por el factor 1,724; pH en relación suelo:agua de 1:2,5 y texura por tamizado y sedimentación (pipeta de Robinson).

Se calculó el valor de Kd de atrazina a partir de la ecuación de Weber et al. (2004) ''Kd = 4,1 + 0,43 MOS + 0,09 ARC -0,81 pH'' [Ec. 1], modelo matemático previamente validado (Becerra et al., 2013). A partir de los datos del muestreo se calculó el Kd correspondiente a cada sitio de muestreo (Kd_m). Para el cálculo del Kd de cada UC se utilizaron dos metodologías: a) según procedimiento descripto en Becerra et al. (2013) que utiliza el promedio ponderado de cada componente de la UC según su porcentaje de participación (Kd_c) y b) considerando solamente la serie predominante de la UC (Kd_p). Utilizando el mapa digital de suelos se calculó el centroide de cada polígono que representa una UC con el software libre QGIS (QGIS Development Team, 2013), asignándole a ese punto el valor Kd_c y Kd_p de la UC que lo contiene. Los centroides de las 518 UC de la provincia de Córdoba a escala 1:500.000 (Fig. 1b) fueron utilizados para realizar interpolaciones y producir mapas de valores continuos de Kd.

Se evaluaron dos métodos de interpolación, kriging ordinario (KO) y kriging universal (KU) cuyos parámetros fueron obtenidos utilizando el paquete geoestadístico geoR (Ribeiro Jr. & Diggle, 2001) en entorno R (R Core Team, 2014). Se evaluaron tres modelos teóricos para ajustar el variograma (esférico, gaussiano y exponencial) utilizando como criterio de selección el de mínima suma de cuadrados ponderados. En todos los casos se comprobó, mediante el histograma, que las distribuciones de las variables a interpolar fueran normales o cercanas a la normal. Para cada sitio de muestreo se calcularon los valores de Kd producto de los diferentes métodos de interpolación; del KO de los valores de Kd_c y Kd_p se obtuvieron valores de Kd_koc y Kd_kop respectivamente, mientras que del KU de los valores de Kd se obtuvieron valores de Kd . En todos c kuc los casos cuando el Kd calculado fue menor a cero, su valor fue reemplazado por 0,01 kg L^-1.

Se realizaron análisis de regresión lineal a fin de determinar el grado de ajuste entre los valores de Kd_m y los estimados a partir de las cartas de suelos (Kd , Kd , Kd , Kd y Kd ); c p koc kop kuc así como también se analizaron las diferencias entre Kd_m y los Kd estimados para cada sitio de muestreo (errores de estimación). Para los análisis estadísticos se utilizó el programa Infostat Kd calculados a partir de datos muestrales y estimados con las cartas de suelos

El rango de valores de Kd_m fue de 0,01 a 4,58 L kg^-1, similar a los de otros estudios para suelos de Córdoba (Hang et al., 2000; Martini, 2008) y Santa Fe (Lenardón et al., 2000, 2002). Este rango fue levemente más amplio que el de Kd_c (0,01 a 4,18 L kg^-1). El valor medio de Kd_m y Kd_c fue similar entre ambos índices, 1,61 ± 1,01 L kg^-1 y 1,63 ± 0,93 L kg^-1, respectivamente. Esta paridad se explica por un efecto compensatorio entre las variables utilizadas para el cálculo dado que el promedio de ARC de los datos muestrales fue mayor al promedio de las cartas de suelos (21% vs 17%) compensado por un mayor pH (6,9 vs 6,3). El promedio de MOS fue similar para los dos casos (2,51 % para el muestreo y 2,55% para las cartas de suelo).

La información de las cartas de suelo puede considerarse vigente ya que las mayores diferencias se dieron en atributos poco variables en el tiempo, como es el caso de ARC (Allred et al., 2008; Berhongaray et al., 2013). Las diferencias de ARC fueron aleatorias (Becerra et al., 2014), por lo cual no se puede considerar un error sistemático asociado a la metodología de determinación. Por otra parte, no se dispone de información de la técnica utilizada para obtener los datos de cartas de suelo, ya que fueron determinados en diferentes épocas y laboratorios. Si bien el pH del suelo puede modificarse en el tiempo, en general se han reportado descensos (Liebig et al., 2002; Vázquez, 2005 citado en Sainz Rosas et al., 2007) o estabilidad en el tiempo (Krüger, 1996; Díaz-Zorita et al., 2004). El reemplazo de la vegetación natural por cultivos ha traído aparejado, en muchos casos, procesos de erosión, salinización y so-dificación (Jayawickreme et al,, 2011) en particular en la zona centro Sur de Córdoba (Canale, 2011), en la cual se encuentra la región SHRQ que se discutirá más adelante.

Análisis por regiones de muestreo

Las medidas resumen de los índices Kd , Kd , Kd calculados para ambos sistemas hidrológicos, SHM y SHRQ, se presentan en la Tabla 1. Los Kd_m correspondientes a cada sistema hidrológico mostraron diferencias sustanciales, con un promedio de 2,03 ± 0,87 L kg^-1 para SHM y 0,79 ± 0,71 L kg^-1 para SHRQ. Estas diferencias fueron esperables ya que los suelos SHM presentaron, en promedio, mayor contenido de MOS y ARC que los de SHRQ (1y 10 puntos porcentuales respectivamente). Los índices obtenidos de cartas de suelos, Kd_c y Kd_p, reprodujeron la misma tendencia.

Para el SHM los índices Kd , Kd y Kd no presentaron diferencias significativas entre ellos, si bien los Kd_m superaron a los otros dos. En los datos del muestreo se identificó mayor contenido de ARC (5 puntos porcentuales) que generó un incremento de 0,48 L kg ^-1 en los valores de Kd que no fue compensado por el mayor pH (0,4 unidades) que provocó un descenso del Kd de 0,36 L kg^-1. Por el contrario, en el SHRQ sí se obtuvieron diferencias significativas (p <0,01) siendo el Kd_m inferior a los índices obtenidos a partir de la cartas de suelo (Kd_c y Kd_p). El pH de muestreo fue superior, en promedio, en 0,8 unidades lo que provocó un descenso de 0,62 L kg^-1 para los Kd, que no fue compensado por el aumento de ARC que sólo incrementó el Kd en 0,23 L kg ^-1.

Tabla 1. Medidas resumen de los Kd calculados con datos muestrales (Kd_m) y estimados a partir de las cartas de suelos (Kd_c y Kd_p) correspondientes los sistema hidrológicos Morteros (SHM) y Río Quinto (SHRQ).
Table 1. Summary statistics of Kd values calculated from sampling data (Kd_m) and estimated from soil survey data (Kd_c y Kd_p) corresponding to Morteros (SHM) and Río Quinto (SHRQ) hydrological units.

n: número de observaciones, DE: desvío estándar, CV: coeficiente de variación; Mín: valor mínimo; Máx: valor máximo; Q1: primer cuartil; Q3: tercer cuartil.

La distribución de frecuencias de los Kd de cada región se muestra en la Figura 2. Los Kd_m de SHM presentaron una distribución cercana a la normal mientras que el histograma de Kd_c fue asimétrico por la derecha. Por su parte, los Kd_m de SHRQ se concentraron en valores próximos a cero mientras que los Kd_c tuvieron un pico cercano a 0,8 L kg^-1. Todos los Kd_m de SHRQ fueron inferiores a 2 L kg^-1 a excepción de un caso cuyo Kd_m fue de 3,5 L kg^-1 debido a su mayor contenido de MOS y particularmente mayor contenido de ARC. La ubicación de este punto sugiere que se trata de una zona de acumulación que explicaría la mayor concentración de MOS y ARC. Descartando ese valor, el Kd_m promedio resultó 0,73 ± 0,58 L kg^-1, y decreció el CV a 80%.

La distribución de los Kd en cada sistema hidrológico presentó diferencias en el rango de valores. En un trabajo previo (Becerra et al., 2013) se establecieron tres categorías de valores de Kd <1,5 L kg^-1 (bajo), 1,5-2,5 L kg^-1 (medio) y >2,5 L kg^-1 (alto). En base a esta clasificación, los valores de Kd de SHM se distribuyeron desde bajos a altos; mientras que en el SHRQ los Kd se concentraron en el rango de valores bajos.

Comparativa entre métodos de estimación

La distribución espacial de los Kd obtenidos de las cartas de suelos para los sitios de muestreo mostró una cierta tendencia creciente en sentido oeste-este asociada a los patrones de distribución de arcilla y materia orgánica. Esta tendencia fue de primer orden (lineal) y fue removida al estimar Kd_kuc en función de Kd_c. Para el ajuste de los semi-variogramas experimentales se probaron tres modelos teóricos: esférico, exponencial y gaussiano. Los modelos de mejor ajuste, que minimizaron la suma de cuadrados y se utilizaron para realizar el kriging, fueron el esférico para el caso de Kd_c y el exponencial para Kd_p y los residuos de Kd_c.

Los valores de Kd estimados según diferentes métodos se presentan en la Tabla 2. Los índices Kd obtenidos por los diferentes métodos no presentaron diferencias significativas para SHM. En el caso de SHRQ, hubo diferencias significativas (p <0,05) entre el Kd_m y todos los métodos de estimación, que no difirieron entre sí.

El análisis de regresión lineal entre los Kd_m y los Kd estimados a partir de datos de las cartas de suelos, mostró mejor ajuste para el caso de las interpolaciones: Kd_koc (R²=0,28), Kd_kop (R²=0,29) y Kd_kuc (R²=0,28) con respecto al uso del mapa de suelos: Kd_c (R²=0,15) y Kd_p (R²=0,12). Entre los diferentes métodos de interpolación no se encontraron mayores diferencias.

Se calculó la diferencia entre el promedio de los Kd_m y el promedio del los Kd promedio estimados. Para el SHM el Kd_m promedio superó en ~ 0,1 L kg^-1 a los Kd estimados, asociado al mayor valor de ARC obtenidos en el muestreo.

Tabla 2. Valores de Kd (L kg^-1) estimados por interpolación por diferentes métodos para el sistema hidrológico Morteros (SHM) y el sistema hidrológico Río Quinto (SHRQ).
Table 2. Kd values (L kg^-1) estimated from different methods corresponding to Morteros (SHM) and Río Quinto (SHRQ) hydrological units.

ri: nùmero de observaciones, DE: desvío estándar, CV: coeficiente de variación; Min: valor mínimo; Máx: valor máximo; Ql: primer cuartil; Q3: tercer cuartil.

Por otra parte, para el SHRQ el valor de Kd_m promedio fue inferior en ~ 0,3 L kg^-1 a los Kd estimados. Esto fue consecuencia de que el promedio de pH de los datos muestrales superó en un punto al de las cartas de suelo (6,8 vs 5,8).

La interpolación por kriging tiende a concentrar los valores hacia la media de la población (Johnston, 2001) lo que explica que los rangos de los Kd interpolados sean más estrechos que los de Kd no interpolados, lo cual también se aprecia en los menores CV (Tabla 1 y 2).

Se calculó el error de predicción para cada sitio de muestreo como la diferencia entre el Kd y los Kd estimados por los diferentes métodos. La distribución de los errores absolutos para cada método se resume en Tabla 3. La interpolación, en sus tres modos (Kd_koc, Kd_kop y Kd_kuc), produjo menores errores (p <0,1), lo que se refleja en un promedio más bajo y un rango de variación más estrecho que se aprecia tanto entre los valores máximos y mínimos como en el rango intercuartílico (Q3 - Q1). Este comportamiento se comprobó tanto para SHM como para SHRQ. Los resultados obtenidos mediante el uso de KO y KU no difirieron entre ellos aún cuando se observó cierta tendencia en los datos.

La representación gráfica de la dispersión entre Kd_m y los errores absolutos (Fig. 5) muestra que las mejores estimaciones se obtuvieron para los valores de Kd intermedios independientemente del método de estimación. La distribución de los errores en función de Kd_m puede ser modelada por una función cuadrática [error (abs) = 1,05 -0,82 Kd + 0,28 Kd ²]. De la ecuación se puede deducir el rango de Kd donde los errores son menores o iguales a 1 L kg^-1, errores considerados bajos ya que causan a lo sumo el cambio de una categoría de adsorción (Becerra et al., 2013). Este rango tiene como valores extremos 0,06 y 2,84 L kg^-1, rango que se extiende a 0,00-2,98 L kg^-1 cuando se consideran sólo las interpolaciones. Los errores mayores a 1 L kg ^-1 fueron menos frecuentes para las interpolaciones (26 casos

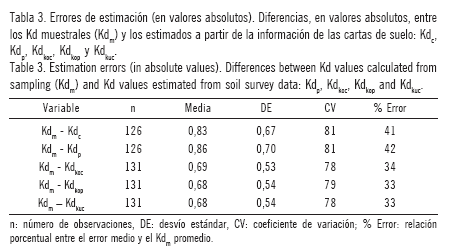
Al comparar los casos en que los Kd_m fueron predichos con errores menores o iguales a 1 L kg^-1(E<1) con los que tuvieron errores mayores a 1 L kg^-1 (E>1) encontramos que para el caso de las interpolaciones hubo diferencias significativas en ARC (p <0,05) y MOS (p <0,01) siendo sus promedios: ARC_E<₁=20,6%, ARC_E>₁₌24,4%; MOS_E<_{1 =} 2,4%; MOS_E>₁=3,0%; mientras que para los métodos no interpolados sólo se encontraron diferencias (p <0,05) en ARC, en donde ARC_E< fue de 20,4% y ARC_E>₁ fue de 23,8%. El pH no presentó diferencias entre los casos con bajos errores de predicción con aquellos de errores mayores.

La escala de los mapas parece ser un factor importante al momento de considerar la conveniencia de la interpolación, ya que estudios previos documentaron que no existieron diferencias significativas entre los mapas temáticos derivados de mapas de suelo de propósito general a escala 1:5000 con los mapas obtenidos por KO a partir de datos muestrales (Bregt etal., 1987). Brus etal. (1996) tampoco encontraron grandes diferencias entre el kriging y la media de las unidades de mapa a escala 1:50.000, remarcando los menores costos de muestreo cuando se emplean las unidades de mapa. Estos resultados alientan el uso de los mapas de suelos ya que componen una amplia base de datos de suelo. Una alternativa que sugieren algunos autores al momento de interpolar, consiste en utilizar la información de los mapas de suelos sobre aspectos geológicos, pedológicos, de relieve, límites naturales, etc. (Heuvelink & Bierkens, 1992; Brus et a/.,1996). Sin embargo, remarcan que estratificar por unidad de mapa y luego krigear internamente tiene dos desventajas, una es que se reducen la cantidad de puntos para calcular el variograma y la otra es que se considera que las unidades están separadas por límites estrictos y por lo general no es así. En nuestro estudio la limitada cantidad de datos por unidad de mapa hizo impracticable evaluar esta metodología.

La distribución espacial de los índices Kd , Kd y Kd correspondientes a SHM y SHRQ se muestran en las Figuras 4 y 5, respectivamente. Los mapas producto de interpolaciones (Kd_koc y Kd_m) muestran una transición gradual entre zonas con diferente adsorción de atrazina debido a la "suavización" de valores característica del kriging (Goo-vaerts, 1997). En estos mapas se puede apreciar claramente las características contrastantes de los dos sistemas hidrológicos, encontrándose en el SHM un predominio de Kd medios con presencia de Kd bajos (Norte y/o Sur según el mapa) y altos (Este), mientras que el SHRQ está dominado ampliamente por Kd bajos.

Figura 4. Distribución espacial, en la región del sistema hidrológico Morteros, de los índices de adsorción de atrazina (Kd) estimados según mapa de unidades cartográficas [Kd_c] (a), interpolación por kriging ordinario de los valores de Kd_c del centroide de cada unidad cartográfica [Kd_koc] (b) y por interpolación por kriging ordinario de valores muestrales [Kd_m] (c).
Figure 4. Spatial distribution of atrazine adsorption indices (Kd) for Morteros hydrological unit area estimated from cartographic units map [Kd_c] (a), kriging interpolation of Kd_c values of the centroid of each cartographic unit [Kd_koc] (b) and kriging interpolation of Kd values calculated from sampling [Kdm] (c).

Figura 5. Distribución espacial, en la región del sistema hidrológico Río Quinto, de los índices de adsorción de atrazina (Kd) estimados según mapa de unidades cartográficas [Kd_c] (a), interpolación por kriging de los valores de Kd_c del centroide de cada unidad cartográfica [Kd_koc] (b) y por interpolación por kriging de valores muestrales [Kd_m] (c).

Figure 5. Spatial distribution of atrazine adsorption indices (Kd) for Río Quinto hydrological unit area estimated from cartographic units map [Kd_c] (a), kriging interpolation of Kd_c values of the centroid of each cartographic unit [Kd_koc] (b) and kriging interpolation of Kd values calculated from sampling

[Kdm] (c).

CONCLUSIÓN

En un estudio previo se sugirió que las cartas de suelos, aún cuando representan una fuente de datos muy útiles para estudios regionales, pueden estar desactualizadas, destacando la necesidad de generar una base de datos actualizada o corroborar la vigencia de dichas cartas.

Nuestros resultados sugieren que a la información provista por las cartas de suelo, aún cuando daten de largo tiempo y a escala de reconocimiento (1:500.000), es posible revalorizarla y ampliar el aporte de este material, si se incorporan métodos de análisis por interpolación. El cálculo del Kd de atrazina a partir de los datos de las cartas de suelo no difirió sustancialmente del obtenido a partir de un muestreo actual.

Las dos zonas analizadas presentaron características diferentes en cuanto a su capacidad de adsorción de atrazina. La zona del sistema hidrológico Morteros tuvo un Kd promedio de 2,0 ± 0,9 L kg^-1, mientras que la zona del sistema hidrológico Río Quinto tuvo una media de 0,8 ± 0,7 L kg^-1.

La estimación del Kd de atrazina a partir de las cartas de suelo resultó más confiable en el rango de Kd de 0,1 a 2,8 L kg^-1. Por encima de 2,8 L kg^-1 los errores de estimación fueron crecientes. La interpolación de la información de los datos de las cartas de suelos condujo a mejores resultados (menores errores de estimación) que el uso de los mapas de suelos por unidad cartográfica (33% y 41% de error respectivamente). El krginguniversal no representó una mejora con respecto al kr/gingordinario, siendo este último un método más sencillo.

AGRADECIMIENTOS

Este trabajo fue financiado mediante proyecto ANPCyT PICT 0250/10.

BIBLIOGRAFÍA

Allred, B; JJ Daniels & MR Ehsani. 2008. Handbook of agricultural geophysics. CRC Press. 432pp.

Becerra, MA; S Hang; M Díaz-Zorita & P Mercuri. 2013. Aplicación de sistemas de información geográfica para la delimitación de áreas con diferente capacidad de adsorción de atrazina. Ciencia del Suelo 31(2): 223-233.

Becerra MA; S Hang; M Díaz-Zorita & G Negro. 2014. Comparación entre datos de las cartas de suelos y de un muestreo. Actas del XXIV Congreso Argentino de la Ciencia del Suelo. Bahía Blanca, 5-9 de Mayo de 2014.

Bellamy, PH; PJ Loveland; RI Bradley; RM Lark & GJD Kirk. 2005. Carbon losses from all soils across England and Wales 1978-2003. Nature 437(7056): 245-248.

Berhongaray, G; R Álvarez; J De Paepe; C Caride & R Cantet. 2013. Land use effects on soil carbon in the Argentine Pampas. Geoderma 192: 97-110.

Bregt, AK; J Bouma & M Jellinek. 1987. Comparison of thematic maps derived from a soil map and from kriging of point data. Geoderma 39(4): 281-291.

Brus DJ; JJ De Gruijter; BA Marsman; R Visschers; AK Bregt; A Breeuwsma & J Bouma. 1996. The performance of spatial interpolation methods and choropleth maps to estimate properties at points: a soil survey case study. Environmetrics 7: 1-16.

Canale, A; A Salafia; P Blanco & R Acotto. 2011. Monitoreo freático para generar estrategias de manejo a escala regional. INTA A.E.R. Laboulaye. Disponible en http://inta.gob.ar/documentos/ monitoreo-freatico-para-generar-estrategias-de-manejo-a-esca-la-regional/. Fecha de consulta 23/10/2014.

Coquet, Y & E Barriuso. 2002. Spatial variability of pesticide adsorption within the topsoil of a small agricultural catchment. Agronomie 22: 389-398.

Di Rienzo, JA; F Casanoves; MG Balzarini; L Gonzalez; M Tablada & CW Robledo 2013. InfoStat versión 2013. Grupo InfoStat, FCA, Universidad Nacional de Córdoba, Argentina. URL http:// www.infostat.com.ar

Díaz-Zorita, M; M Barraco & C Álvarez. 2004. Efectos de doce años de labranzas en un Hapludol del Noroeste de Buenos Aires, Argentina. Ciencia del Suelo 22(1): 11-18.

Elabd, H; WA Jury & MM Cliath. 1986. Spatial variability of pesticide adsorption parameters. Environ Sci Technol. 20: 256-260.

GeoINTA. 2012. SAGyP - INTA - Proyecto PNUD ARG/85/019. Suelosde la República Argentina v.9. Disponible en http:// geointa.inta.gov. ar/

Goovaerts, P & A Journel. 1995. Integrating soil map information in modelling the spatial variation of continuous soil properties. European Journal of Soil Science 46: 397-414.

Goovaerts, P. 1997. Kriging vs stochastic simulation for risk analysis in soil contamination. En: geoENV I - Geostatistics for Environmental Applications. Pp.247-258.

Hang, S; M Bocco & R Sereno. 2000. Adsorción de atrazina en dos perfiles de suelos argentinos, bajo siembra directa Agrochimica44(3- 4): 115-122.

Henríquez C; R Killorn; F Bertsch & F Sancho. 2005. La geostadística en el estudio de la variación espacial de la fertilidad del suelo mediante el uso del interpolador kriging. Agronomía Costarricense 29: 73-81.

Heuvelink GBM & MFP Bierkens. 1992. Combining soil maps with interpolations from point observations to predict quantitative soil properties. Geoderma 55(1): 1-15.

Jayasundera, S; WJ Schmidt; CJ Hapeman & A Torrents. 2000. What's known and what's yet to be known with respect to the sorption of organic pollutants onto soils. Revista Internacional de Contaminación Ambiental 16: 147-156.

Jayawickreme, D; C Santoni; J Kim; E Jobbagy & R Jackson. 2011. Changes in hydrology and salinity accompanying a century of agricultural conversion in Argentina. Ecological Applications 21(7): 2367-2379.

Johnston, K.; JM Ver Hoef; K Krivoruchko & N Lucas. 2001. Using ArcGIS Geostatistical analyst. Environmental Systems Research Institute, Redlands, CA.

Krüger, HR. 1996. Sistemas de labranza y variación de propiedades químicas en un Haplustol Entico. Ciencia del Suelo 14: 53-55.

Lenardón, A; M Maitre; S Enrique & V Bernasconi. 2000. Extracción y cuantificación de atrazina en el suelo. Actas del XVII Congreso Argentino de la Ciencia del Suelo, Mar del Plata, Argentina, Abril 11-14.

Lenardón, A; M Maitre; E Lorenzatti; P De la Sierra; F Marino & S Enrique. 2002. Plaguicidas en diversos medios: experiencias y resultados. II Taller de Contaminación por Agroquímicos. Pergamino, Argentina. Disponible en: http://www.inta.gov.ar/parana/info/docu-mentos/suelos/contamina/Lenardon.pdf

Liebig, MA; GE Varvel; JW Doran & BJ Wienhold. 2002. Crop sequence and nitrogen fertilization effects on soil properties in the western corn belt. Soil Science Society of America Journal 66(2): 596-601.

López, FF; C Durán & S Benítez. 1981. Importancia de la cartografía en las ciencias agropecuarias. Revista de la Universidad Católica. Pontificia Universidad Católica del Ecuador 29: 35-46.

Manchanda, ML; M Kudrat & AK Tiwari. 2002. Soil survey and mapping using remote sensing. Tropical Ecology 43(1): 61-74.

Martini, PL. 2008. Estudio del comportamiento de Atrazina en suelos agrícolas de la Pcia. de Córdoba y su relación con la estratificación de la materia orgánica provocada por la siembra directa. Tesis de Maestría. EG-FCA-UNC.

Petersen, GW; JC Bell; K Mcsweeney; GA Nielsen & PC Robert. 1995. Geographic information systems in agronomy. AdvAgr. 55: 67-111.

QGIS Development Team.2013. QGIS Geographic Information System. Open Source Geospatial Foundation Project. http:// qgis.osgeo.org

R Core Team. 2014. R: A language and environment forstatistical computing. R Foundation for Statistical Computing,Vienna, Austria. URL http://www.R-project.org/

Ribeiro Jr, PJ & PJ Diggle. 2001 geoR: A package for geostatistical analysis. R-NEWS Vol 1, No 2. ISSN 1609-3631.

Sainz-Rosas, H; H Echeverría & H Angelini. 2007. Niveles de materia orgánica y pH en suelos agrícolas de la región pampeana y extrapampeana argentina. IPNI. Informaciones Agronómicas 2: 6-12.

Schipper LA; WT Baisden; RL Parfitt; C Ross; JJ Claydon & G Arnold. 2007. Large losses of soil C and N from soil profiles under pasture in New Zealand during the past 20 years. Global Change Biology 13: 1138-1144.

Sonneveld, MPW; J Bouma & A Veldkamp. 2002. Refining soil survey information for a Dutch soil series using land use history. Soil Use and Management 18(3): 157-163.

SsRH (Subsecretaría de Recursos Hídricos de la Nación). 2011. Atlas de Cuencas y Regiones Hídricas Superficiales de la República Argentina - Versión 2010.

Stevens A & B Van Wesemael. 2008. Soil organic carbon dynamics at the regional scale as influenced by land use history: a case study in forest soils from southern Belgium. Soil Use and Management 24: 69-79.

Vázquez, ME. 2005. Calcio y Magnesio, acidez y alcalinidad del suelo. En: Fertilidad de Suelos y Fertilización de Cultivos (edsHE Echeverría & FO García). Ediciones INTA, Buenos Aires, Argentina. p. 161-188.

Wagenet, RJ; J Bouma & RB Grossman. 1991. Minimum data sets for use of soil survey information in soil interpretive models. En: Spatial Variabilities of Soils and Landforms. pp 161-182.

Weber, J; G Wilkerson & C Reinhardt. 2004. Calculating pesticide sorption coefficients (Kd) using selected soil properties. Chemosphere 55: 157-166.