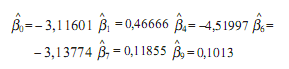[article pii="nd" doctopic="oa" language="es" ccode="conicyt" status="1" version="4.0" type="gra tab" order="11" seccode="cds010" sponsor="nd" stitle="Cienc. suelo" volid="34" issueno="2" dateiso="20161200" fpage="293" lpage="301" pagcount="9" issn="1850-2067"]MANEJO Y CONSERVACIÓN DE SUELOS Y AGUAS. RIEGO Y DRENAJE
[front][titlegrp][title language="es"]Modelo ‘‘cuanti-cualitativo’’ de escurrimiento superficial del agua en suelos agrícolas de la región Pampeana Argentina[/title][/titlegrp]
[authgrp][author role="nd" rid="a01" corresp="n" deceased="n" eqcontr="nd"][fname]JOSÉ MIGUEL[/fname] [surname]ANDRIANI[/surname][/author]1*; [author role="nd" rid="a01" corresp="n" deceased="n" eqcontr="nd"][fname]LUCIANA[/fname] [surname]MAGNANO[/surname][/author]1 & [author role="nd" rid="a01" corresp="n" deceased="n" eqcontr="nd"][fname]NICOLÁS[/fname] [surname]SANMARTI[/surname][/author][/authgrp]1
1 [aff
id="a01" orgname="Instituto Nacional de Tecnología
Agropecuaria" orgdiv1="EEA Oliveros Grupo" orgdiv2="Área de
Agronomía"]INTA-Instituto Nacional de Tecnología Agropecuaria. EEA
Oliveros Grupo, Área de Agronomía[/aff]
* Autor de contacto: andriani.jose@inta.gob.ar
[bibcom][hist]Recibido: [received
dateiso="20160222"]22-02-16[/received]
Recibido con revisiones: [revised
dateiso="20160812"]12-08-16[/revised]
Aceptado: [accepted dateiso="20160812"]12-08-16[/accepted][/hist]
RESUMEN
[abstract language="es"]Desde hace mucho tiempo se está estudiando la modelación de la relación lluvia-escurrimiento y han sido desarrollados una gran cantidad de métodos y modelos para simular la generación de escurrimiento de una lluvia. Uno de los métodos ampliamente usados es el ‘‘Número de Curva’’ (NC) del Servicio de Conservación de Suelo de Estados Unidos, que tiene la dificultad de necesitar datos empíricos. Tanto éste, como todos los modelos de regresión producen resultados muy variables ante un mismo evento de lluvia. Por tal motivo, se planteó desarrollar un modelo cuanti-cualitativo, que ayude a disminuir esa variabilidad, sobre la base de un modelo de regresión cuantitativo ajustado para la Región Pampeana Argentina. Con el conjunto de datos cuantitativos se efectuó un análisis de regresión, y posteriormente se los asoció con datos cualitativos. El objetivo del análisis fue poder determinar valores medios de escurrimiento a partir de la cantidad de lluvia caída, la intensidad de la misma y la humedad superficial del suelo. Para estimar el escurrimiento en función de variables cuantitativas y cualitativas, se utilizó un modelo de regresión lineal múltiple con variables indicadoras. A partir del mismo se utilizó el proceso de selección de variables Backward, para seleccionar cuáles son las variables que deben quedar en el modelo. Para suelos Molisoles de aptitud agrícola en siembra directa de la Región Pampeana, la ecuación lineal obtenida de los datos observados, presenta un buen ajuste estadístico. Sin embargo, la variabilidad encontrada en valores de precipitación diaria entre los 40 y 80 mm, no es admisible para la estimación de balances hídricos de cultivos. Para los suelos mencionados, el modelo de regresión obtenido con variable cuantitativa y variables indicadoras cualitativas produce una mejora sustancial para la estimación del escurrimiento superficial.[/abstract]
Palabras clave: [keygrp scheme="nd"][keyword type="m" language="es"]Relación precipitación-escurrimiento[/keyword]; [keyword type="m" language="es"]Métodos de cálculo[/keyword]; [keyword type="m" language="es"]Intensidad de lluvia[/keyword]; [keyword type="m" language="es"]Ecuaciones[/keyword][/keygrp].
Quantitative - qualitative surface runoff model in agricultural soils of the Argentine Pampeana Region
ABSTRACT
[abstract language="en"]Rainfall-runoff relationship modeling have been studied for a long time, developing along these period several methods and models to simulate rainfall-runoff event. One of the widely used methods is the ‘‘Curve Number’’ (CN) of the United States Soil Conservation Service which requires empiric data. This method as well as all regression models provides highly variable results for the same rainfall event. Therefore, in order to find a quantitative and qualitative model that helps reduce these variability, a quantitative adjusted regression model for Argentine Pampa Region is proposed. It was performed a regression analysis with a set of quantitative data, subsequently became associated with qualitative data. The objective of the analysis was to determine runoff average values from both the quantity and intensity of rainfall, and the surface soil moisture. A multiple linear regression model with variable indicators was used to estimate runoff based on quantitative and qualitative variables. A Backward Selection process was used to select variables that should be in the model. The linear equation obtained from the observed data, for non-tillage Mollisols with agricultural aptitude of the Pampa Region with slopes less than 1%, had good statistical adjustment. However, the variability found in daily precipitation values between 40 and 80 mm, is not suitable for estimating crop water balances. In summary, the soil described showed that the regression model with quantitative and qualitative indicator variables produces a substantial improvement for surface runoff estimation.[/abstract]
Key words: [keygrp scheme="nd"][keyword type="m" language="en"]Rainfall-runoff relationship[/keyword]; [keyword type="m" language="en"]Calculation methods[/keyword]; [keyword type="m" language="en"]Rainfall intensity[/keyword]; [keyword type="m" language="en"]Equation[/keyword][/keygrp][/bibcom].[/front]
[body]INTRODUCCIÓN
Hace tiempo que se viene estudiando la
modelación de la relación lluvia-escurrimiento. La historia de esta relación se
conoce desde hace más de 300 años, con el reporte de las mediciones
cuantitativas en hidráulica, publicado por P. Perreault en 1674 (Linsley,
1982), el que estableció la relación funcional Qa = Pa/6.
Donde Qa es el caudal o escorrentía de la cuenca y Pa es
la precipitación del área en estudio o cuenca.
La forma básica de todos los modelos hidrológicos disponibles (Mishra y Singh,
2003) puede, en general, expresarse como:
Q = P - L
donde: Q es la escorrentía, P es la
precipitación y L es la abstracción hidráulica de la cuenca, entendida como el
conjunto de infiltración, almacenaje, retención superficial, intercepción,
evaporación y evapotranspiración.
A partir de esta ecuación, han sido desarrollados una cantidad de métodos y
modelos para simular la generación de escurrimiento de una lluvia. Uno de los
métodos ampliamente usados es el ‘‘Número de Curva’’
(NC) del Servicio de Conservación de Suelo de Estados Unidos (SCS, 1972). Este
es un modelo conceptual apoyado por información empírica. La mayoría de los
elementos de un proceso de lluvia-escurrimiento están incorporados en el método
de NC tales como: Característica de la cuenca, precipitación, abstracción
hidráulica y escurrimiento. El NC es utilizado fundamentalmente en cuencas
hidrológicas, aunque también se lo ha incorporado a modelos de producción de
cultivos como los DSSAT (Jones et al., 2003). Sin embargo, Pellat (2009)
sostuvo que, pese a ser ampliamente usado en todo el mundo, modificando la
relación de abstracción, esta ecuación da una falsa apariencia de
funcionalidad.
Cuando nos enfocamos en un lote de producción agrícola, los principales
parámetros a tener en cuenta para obtener el valor L, del modelo
lluvia-escurrimiento, son la intensidad de la precipitación, el contenido de
agua en el suelo, la pendiente y la cobertura superficial (Mishra y Singh,
2003). Generalmente, para querer representar estas áreas de producción, el
valor L es obtenido por la diferencia P - Q, utilizando parcelas de
escurrimiento. La FAO (Hudson, 1997) estableció tres tipos de parcelas de
escurrimiento de acuerdo al objetivo buscado, i) micro-parcelas de 1 o 2 m2
para una simple comparación de dos tratamientos, ii) parcelas pequeñas de
alrededor de 100 m2, para prácticas de cultivo y cobertura, iii)
parcelas grandes de aproximadamente una hectárea, para evaluación de tipo de
terrazas o efecto de pastoreo. Investigaciones realizadas en INTA EEA Paraná
(Sasal et al., 2010), EEA Pergamino y EEA Marcos Juárez, utilizaron
parcelas pequeñas FAO, con pendiente 2% y 3,5%. También otras de alrededor de
1500 m2 con 1% de pendiente, para determinar la pérdida de agua y
esencialmente la pérdida de suelo y nutrientes. De esta manera, se puede
ajustar el valor L, para un determinado tipo de suelo y uso de la tierra. Sin
embargo, no se puede generalizar el resultado de estas parcelas para la
evaluación del escurrimiento superficial diario, en los lotes de producción de
cultivos de una gran región, debido a que las mismas fueron construidas para
evaluar la erosión hídrica del suelo y la cantidad total de agua perdida en
determinadas condiciones de pendiente y uso de la tierra.
Casi todos los suelos agrícolas de la Región Pampeana argentina pertenecen al
Orden de los Molisoles, y dentro de estos, predominan los Grandes Grupo de los
Argiudoles, Hapludoles y Haplustoles (Panigatti, 2010; Godagnone et al.,
2002). Desde el punto de vista de la producción agrícola y en especial cuando
queremos elaborar un balance hídrico de cultivo, el escurrimiento de agua
superficial fuera del área del cultivo es un factor cuantitativamente
importante en regiones de secano. De ahí, la necesidad de contar con un modelo
confiable que estime con buena precisión las situaciones reales de la relación
precipitación-escurrimiento. En realidad, para el cultivo lo más importante es
la precipitación efectiva (PE) que gobierna la disponibilidad de agua en el
suelo, y la evapotranspiración. Entonces, estos serían los componentes de L a
tener en cuenta, mientras que la retención superficial y la
intercepción-evaporación, estarían incluidas en el escurrimiento, entendiéndolo
como la cantidad de agua que sale del sistema.
Dardanelli et al. (2010) obtuvieron una ecuación cuantitativa de
escurrimiento superficial (ES) en función de las precipitaciones diarias,
midiendo los valores reales de agua infiltrada en el suelo (PE) con lecturas de
sonda de neutrones antes y después de un evento de lluvia, en las regiones
centro-este de Córdoba y sur de Santa Fe. Si bien, la ecuación cuantitativa
obtenida presentaba un alto valor de R2, también presentaba amplios
rangos de dispersión en valores medios y altos de precipitación diaria. En
consecuencia, la utilización de la misma en zonas de intensas precipitaciones,
con altos valores diarios, produce importantes errores en el cálculo del
balance hídrico. Seguir buscando disminuir la variabilidad de los valores ES
con modelos cuantitativos va a ser una tarea difícil. Por lo tanto, es
necesario considerar la alternativa práctica y universal de variables
cualitativas.
Definidos el tipo de suelo y la pendiente, otros dos factores que afectan el ES
diario son la intensidad de la precipitación (IP) y el estado de humedad
superficial del suelo (HSS), los cuales podrían ser utilizados como variables
cualitativas.
Por consiguiente se planteó la hipótesis, que la variabilidad del escurrimiento
superficial diario encontrada en los modelos cuantitativos se disminuye con
modelos cuanti-cualitativos que incorporan variables indicadoras de IP y HSS.
Para confirmar esta hipótesis se establecieron los objetivos de: i) Ampliar el
número de observaciones de la ecuación de escurrimiento superficial obtenida
por Dardanelli et al. (2010) como modelo cuantitativo para pendientes
menores a 1%. ii) Obtener un modelo cuantitativo para pendientes entre 1% y 2%.
iii) Encontrar modelos cuanti-cualitativos de escurrimiento superficial que
contengan las variables indicadoras de intensidad de lluvia y humedad
superficial del suelo.
MATERIALES Y MÉTODOS
La experiencia se llevó a
cabo en la INTA-EEA Oliveros (32°33’S - 60°51’W), sobre suelos
serie Maciel y Oliveros (Andriani, 2006), y en Berreta (32°57’S -
61°24’W) sobre un suelo serie Correa; todos pertenecientes al Gran Grupo
de los Argiudoles y cultivados en el sistema de siembra directa. En el caso de
la EEA Oliveros se evaluaron cuatro lotes de producción agrícola desde los años
2010 al 2014, con pendientes menores al 1% y en Berreta sobre un solo lote
desde 2006 al 2009, con pendientes entre el 1 y 2%. En cada lote se colocaron
tres tubos de aluminio de dos metros de profundidad en los sectores más
representativos del relieve. Estos tubos fueron utilizados para medir la
humedad del suelo en el punto medio de cada horizonte con una sonda de
neutrones, marca Troxler, modelo 4302. En Oliveros las lecturas de humedad del
suelo se realizaron el día anterior y posterior de cada evento de lluvia.
Mientras que en Berreta, las lecturas se realizaron en períodos entre 15 y 21
días, seleccionándose los períodos que tuvieron eventos de lluvias únicos,
ajustándose los valores registrados con la evapotranspiración del cultivo (ETC)
o evaporación del barbecho (E). Para obtener el dato de escurrimiento puntual,
se utilizó la ecuación general de escurrimiento (Q=P-L) para cada evento de
lluvia superior a 5 mm, reemplazando el valor L por PE. La PE se calculó como
la diferencia entre dos mediciones sucesivas de humedad de suelo (antes y
después de la lluvia), menos la ETC o E, en ese período. La ETC se calculó
multiplicando el coeficiente de cultivo (Kc) (Andriani, 1999 y datos no
publicados) por la evapotranspiración de referencia (ETo), utilizando la
fórmula de Penman-Monteith (Allen et al., 2006), para el cálculo de esta
última. Los registros de lluvia diaria se tomaron de pluviómetros ubicados
cerca de los lugares de muestreo y los demás parámetros meteorológicos (para el
cálculo de ETo) fueron obtenidos de la estación meteorológica de la EEA
Oliveros.
Los datos ES diarios obtenidos de esta experiencia se agregaron a los datos
presentados por Dardanelli et al. (2010). Para explicar
cuantitativamente el comportamiento del escurrimiento superficial diario se
ajustó un modelo de regresión lineal simple, utilizando como variable
explicativa la precipitación diaria. La recta de regresión en su intersección
con el eje de las abscisas, determinó el valor de lluvia diaria a partir del
cual, el escurrimiento superficial es positivo.
De esa estación meteorológica, también se utilizaron las fajas del pluviógrafo,
realizándose lecturas horarias. En base a estas lecturas se establecieron tres
niveles cualitativos de intensidad de lluvia diaria: Suave, moderada e intensa,
a partir de eventos que tuvieran precipitaciones menores a 6 mm/h, entre 6 y 15
mm/h y superiores a 16 mm/h, respectivamente. Otro aspecto cualitativo que se
tuvo en cuenta, fue el estado de humedad superficial del suelo. Este aspecto es
subjetivo, pero estuvo basado en la apreciación que normalmente realiza el
productor agrícola en su observación habitual del estado de humedad de la
superficie del suelo. Se lo clasificó teniendo en cuenta su estado en el
momento previo a la lluvia: húmedo (no apropiado para utilizar maquinaria agrícola),
oreado (está óptimo para la siembra) y seco (la superficie se la ve
completamente seca).
Con el conjunto de datos cuantitativos clasificados como se señaló
anteriormente, se realizó un análisis estadístico. El objetivo del análisis fue
poder determinar valores medios de escurrimiento a partir de la cantidad de
lluvia caída, la intensidad de la misma y la humedad superficial del suelo.
Para estimar el escurrimiento en función de variables cuantitativas y
cualitativas, se utilizó un modelo de regresión lineal múltiple con variables
indicadoras (Neter et al., 1996), donde dichas variables toman el valor
uno cuando el atributo al que se hace referencia está presente y valor cero en
caso contrario (Tabla 1).
Tabla 1. Valores de variables indicadoras
para intensidad de lluvia y humedad superficial del suelo.
Table 1. Indicator variables
values for rainfall intensity and surface soil moisture.

El modelo planteado tiene la siguiente forma:
A partir de (1), se especificó un modelo distinto para cada combinación de los niveles de intensidad de las precipitaciones y niveles de humedad del suelo (Tabla 2).
Tabla 2. Niveles de intensidad de las
precipitaciones y humedad superficial del suelo.
Table 2. Levels of rainfall intensity and surface soil moisture.

Por ejemplo, para el caso en que la intensidad de las precipitaciones sea intensa y el suelo seco, la ecuación (1) tomará la siguiente expresión:
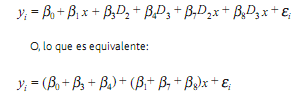
A partir del planteo del modelo (1) se utilizó el proceso de selección de variables Backward (Neter et al., 1996) para seleccionar cuáles son las variables que deben quedar en el modelo. Dicho procedimiento comienza con un modelo que tiene todas las variables regresoras y va eliminando las variables menos influyentes.
RESULTADOS Y DISCUSIÓN
Se obtuvieron de este trabajo 40 datos de
ES, en suelos con pendientes menores al 1%, que sumados a los publicados por
Dardanelli et al. (2010), completaron un total de 120 datos. Estos son
graficados en la Figura 1, en relación con la precipitación
diaria correspondiente, y ajustados a una ecuación lineal de regresión, cuyo R2
fue de 0,83.
El modelo estimado que representa la relación entre la precipitación diaria y
el escurrimiento superficial para pendientes del suelo inferiores al 1% (Fig. 1) es el siguiente:
Q = 0,5954 P - 8,5643 (2)
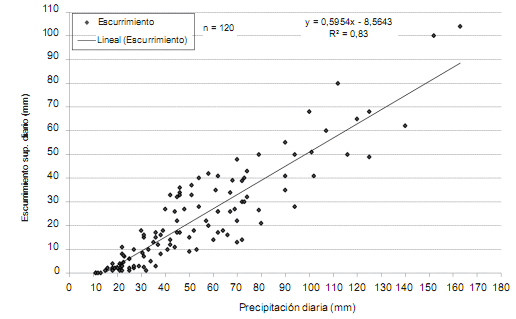
Figura 1. Relación entre la precipitación
diaria y el escurrimiento superficial diario, para suelos Molisoles bajo
siembra directa. Suelos con pendientes menores al 1%.
Figure 1. Relationship between daily rainfall and daily surface runoff,
under non-tillage in Mollisols soils. Soils slopes less than 1%.
donde, P es la precipitación diaria y Q el
escurrimiento superficial.
Si bien, el valor de R2 de esta ecuación lo podemos considerar como
un buen indicador de la bondad del modelo para explicar la variabilidad del
escurrimiento (dispersión de los datos), se puede observar que la mayor
dispersión se encuentra entre los valores de 40 y 80 mm de precipitación diaria
(Fig. 1). Cuando por separado se analizan los 51 datos que
se encuentran dentro de este rango, el R2 que se obtiene es de 0,11.
En regiones donde la probabilidad de ocurrencia de este rango de
precipitaciones es alta, los errores que se pueden cometer en la estimación del
ES diario, suelen ser muy grandes.
Por otra parte, se puede observar en la Figura 1, que la línea
de regresión de esos puntos toca el eje de las abscisas en el valor de
precipitación diaria de 14 mm. Por lo tanto, que valores inferiores a esa
cantidad de precipitación no producen escurrimiento superficial.
Como se mencionó en la introducción la relación lluvia diaria-escurrimiento
superficial se está estudiando desde hace muchos años, en la mayoría de los
casos para estudios hidráulicos y no para lotes de producción agrícola. En la
producción agrícola, el número de curva es la ecuación más difundida en todo el
mundo, principalmente en los modelos de simulación de producción de cultivos
(Jones et al., 2003) y en el balance de agua en el suelo. Sin embargo,
por más que se obtengan los datos empíricos del lugar (ajustando a algún número
de curva), adolece principalmente de su baja sensibilidad a la variabilidad de
la intensidad de lluvia. Pellat (2009) menciona que después de varios años de
uso del método del NC de forma indiscriminada (validada muy pocas veces; y
cuando esto es así, sólo se comporta bien cuando P es muy grande), es
imperativa una formulación hidrológicamente sólida entre P y Q, en un esquema
simple similar al formato del NC. Coincidiendo con lo que decía Mishra et al.
(2005), que el seguir buscando darle solidez al método a través de relaciones
empíricas o adecuaciones ‘‘ad hoc’’, es parte de hacer
viable un absurdo sin bases teóricas. Tanto Pellat, como Dardanelli et al.
(2010) proponen otros tipos de modelos simples exponenciales, uno con sustento
hidrológico y otro basado en registros locales, respectivamente.
El modelo cuantitativo de ES (2), como todos aquellos que se utilizan en la
determinación de balances hídricos, no presenta una estimación aceptable de los
datos reales de ES, en valores altos de precipitación diaria (más de 40 mm).
Por lo tanto, para mejorar esta estimación se propuso utilizar variables
indicadoras cualitativas.
A partir del modelo presentado en (1) se hizo una selección de variables
utilizando el procedimiento Backward. El modelo resultante de dicha selección es
el que se presenta a continuación:
Los valores obtenidos para los estimadores paramétricos fueron:
Una vez determinado el modelo (3) se especificaron los modelos para cada uno de los escenarios de intensidad de la precipitación y humedad superficial del suelo. Por ejemplo, en el caso en que la precipitación es moderada y el suelo oreado, el modelo que se utiliza es:
Cuando la precipitación es suave y el suelo húmedo, la ecuación resultante es:
Así, para cada uno de los escenarios presentados se calculó el valor del escurrimiento medio estimado. Una forma más simple de estimar el escurrimiento, tomando como ejemplo este caso, es utilizando la ecuación:
![]()
donde, x es la precipitación diaria y los
coeficientes b0 y b1 (Tabla 3)
resumen los B y D que se deben incorporar en cada escenario (combinación de IP
y HSS).
Es decir, según el ejemplo anterior,
Tabla 3. Coeficientes para estimar el
escurrimiento medio en los distintos escenarios de intensidad de precipitación
y estado de humedad superficial del suelo.
Table 3. Coefficients to estimate
average runoff in different rainfall intensity scenarios and surface soil
moisture status.

A cada uno de los 120 valores observados de escurrimiento superficial, asociados a determinados valores de precipitación diaria (Fig.1), se le adjuntaron los valores ajustados obtenidos por los modelos de regresión múltiple con variables indicadoras, correspondientes a cada categoría (Fig. 2).

Figura 2. Comparación de los valores de
escurrimiento superficial observados a campo y los valores estimados por los
modelos para cada uno de los escenarios encontrados. Suelos con pendientes menores al 1%.
Figure 2. Comparison of surface runoff observed field values and models
estimated values for each scenario. Soils slopes less than 1%.
Mientras que el modelo de regresión lineal
simple presentado en la Figura 1 explica el 83% de la
variabilidad de la variable escurrimiento, el modelo de regresión con variables
indicadoras explica el 96% de dicha variabilidad. Es decir, que los valores
ajustados explican más la variabilidad de los datos observados que la curva de
regresión de la Figura 1. También, se calculó la raíz del
error cuadrático medio y los valores resultaron ser: 8,8 para el modelo de
regresión simple y 3,9 para el modelo con variables indicadoras. Es decir,
estos resultados ponen de manifiesto la importancia que tiene considerar en el
modelo los dos factores evaluados.
Otra manera de presentar los datos es observar cuanto se aproximan los valores
ajustados a los observados (Fig. 3). Si el modelo ajusta
correctamente a los datos observados, la mayoría de los puntos deben estar en o
cercanos a la línea sólida correspondiente a la función identidad.

Figura 3. Relación entre valores observados y
valores predichos.
Figure 3. Relationship between observed values and predicted values.
Los resultados que se obtengan de las
ecuaciones del modelo cuanti-cualitativo pueden presentar valores negativos
para un determinado rango de valores de precipitaciones. Si bien se estableció
un valor límite de precipitación de 14 mm por encima del cual comienza a haber
ES, este es un valor promedio de las distintas condiciones de IP y HSS. Por
consiguiente, en todos los casos que se utilice este modelo y se obtengan
valores de ES iguales o menores a cero, significa que no hay escurrimiento
superficial y toda agua precipitada ingresa al suelo.
En la localidad de Berreta, sobre un lote de producción agrícola con una
pendiente entre 1 y 2%, se obtuvieron 27 datos de escurrimiento superficial. En
la Figura 4 se grafican esos datos en función a su
respectiva precipitación diaria y ajustados a una línea de regresión, cuyo R2
fue de 0,92. En el gráfico de esta figura, se puede observar que la línea de
regresión de esos puntos toca el eje de las abscisas en el valor de
precipitación diaria de 12 mm. Por lo tanto, valores inferiores a esa cantidad
de precipitación no producen escurrimiento superficial.

Figura 4. Relación entre la precipitación diaria
y el escurrimiento superficial diario, para suelos Argiudoles bajo siembra
directa. Suelos
con pendientes entre el 1 y 2%.
Figure 4. Relationship between daily rainfall and daily surface runoff,
under non-tillage in Argiudolls soils. Soils slopes between 1 and 2%.
El modelo cuantitativo que representa la relación entre la precipitación diaria y el escurrimiento superficial, para esa condición, es el siguiente:
donde, P es la precipitación diaria y Q el escurrimiento superficial.
Para un mismo valor de precipitación
susceptible de escurrimiento, los valores de ES estimados con esta ecuación son
superiores a los que se obtienen con la ecuación (1) en pendientes menores.
Esto era de esperar, ya que Weir (2002) había comprobado que pendientes
superiores al 1% provocaban una pérdida de agua por ES de alrededor de 2,5
veces mayor que pendientes inferiores al 1%.
Se observó que el análisis del modelo de regresión lineal múltiple con
interacciones (1) para los 27 datos obtenidos iba a ser muy inconsistente.
Debido a que, dentro de las distintas combinaciones cualitativas (Tabla 1), una de ellas no contaba con valores y varias tenían
muy pocos datos. Por consiguiente, se decidió presentar solamente el modelo
cuantitativo (4).
CONCLUSIONES
Para suelos Molisoles de aptitud agrícola en
siembra directa de la Región Pampeana Argentina, con pendientes inferiores al
1%, la ecuación lineal obtenida de los datos observados, presenta un buen
ajuste estadístico. Sin embargo, no presenta una estimación aceptable de los
datos reales de ES, para precipitaciones diarias entre los 40 y 80 mm,
frecuentes en esta región.
El modelo cuanti-cualitativo, utilizando variables indicadoras de intensidad de
las precipitaciones y estado de humedad superficial del suelo, produce una
mejora sustancial respecto al modelo cuantitativo para la estimación del
escurrimiento superficial y su uso en modelos de balance hídrico de cultivos.
En el caso que este modelo produzca valores de ES iguales o menores que cero,
se debe considerar que no hubo escurrimiento y que toda el agua precipitada
ingresó al suelo.
Este último modelo tiene validez para suelos agrícolas en siembra directa de la
Región Pampeana con pendientes menores al 1%, ya que fue desarrollado sobre el
modelo cuantitativo mencionado anteriormente, y dado que esta región posee
característica de intensidad de eventos de precipitaciones diarias muy similares.
Considerando lo anteriormente dicho, la aplicación y utilización del modelo
cuanti-cualitativo podría ser extensible a todo el país, teniendo en cuenta que
sean suelos Molisoles en siembra directa, con pendiente inferior al 1%.
Para suelos Molisoles de aptitud agrícola en siembra directa del sur de Santa
Fe, con pendientes entre el 1 y 2%, el modelo cuantitativo obtenido mostró un
muy buen ajuste pese a los pocos datos registrados de ES, pudiendo ser una
buena referencia para estos suelos. Esos pocos datos fueron muy escasos para
conseguir un modelo cuanti-cualitativo.[/body]
[back]AGRADECIMIENTOS
Al señor Carlos Correro por su extraordinaria predisposición y dedicación en el registro de datos tomados a campo. Este trabajo se pudo realizar por financiación y logística aportada por el Instituto Nacional de Tecnología Agropecuaria.
BIBLIOGRAFÍA
[other standard="other" count="15"][ocitat][no]1[/no]. [omonog][oauthor role="nd"][surname]Allen[/surname], [fname]RG[/fname][/oauthor]; [oauthor role="nd"][fname]LS[/fname] [surname]Pereira[/surname][/oauthor]; [oauthor role="nd"][fname]D[/fname] [surname]Raes[/surname][/oauthor] & [oauthor role="nd"][fname]M[/fname] [surname]Smith[/surname][/oauthor]. [date dateiso="20060000" specyear="2006"]2006[/date]. [title language="es"]Evapotranspiración del cultivo[/title] - [subtitle]Guías para la determinación de los requerimientos de agua de los cultivos[/subtitle]. [coltitle]Cuadernos de riego y drenaje[/coltitle] N° 56. [pubname]FAO[/pubname], [city]Roma[/city], [extent]298 pp[/extent][/omonog].[/ocitat]
[ocitat][no]2[/no]. [ocontrib][oauthor role="nd"][surname]Andriani[/surname], [fname]JM[/fname][/oauthor]. [date dateiso="19990000" specyear="1999"]1999[/date]. [title language="es"]Coeficientes de cultivo para soja de distinta época de siembra[/title].[/ocontrib] [omonog][confgrp][confname]Mercosoja 99[/confname], Resumen de trabajos y conferencias presentadas, [city]Rosario[/city], [country]Argentina[/country]. Ecofisiología y Climatología,[/confgrp] pp. [pages]1[/pages][/omonog].[/ocitat]
[ocitat][no]3[/no].. [ocontrib][oauthor role="nd"][surname]Andriani[/surname], [fname]JM[/fname][/oauthor] [date dateiso="20060000" specyear="2006"]2006[/date]. [title language="es"]Contenido de agua útil de los principales suelos Argiudoles y Hapludoles del sur de Santa Fe[/title].[/ocontrib] [omonog][confgrp][no]XX[/no] [confname]Congreso Argentino de la Ciencia del Suelo, I reunión de suelos de la región andina[/confname], resúmenes, [state]Salta[/state]-Jujuy[/confgrp], Argentina, pp. [pages]94[/pages][/omonog].[/ocitat]
[ocitat][no]4[/no]. [ocontrib][oauthor role="nd"][surname]Dardanelli[/surname], [fname]J[/fname][/oauthor]; [oauthor role="nd"][fname]I[/fname] [surname]Severina[/surname][/oauthor] & [oauthor role="nd"][fname]JM[/fname] [surname]Andriani[/surname][/oauthor]. [date dateiso="20100000" specyear="2010"]2010[/date]. [title language="es"]Funcionalidad de raíces y agua del subsuelo[/title]: [subtitle]Su rol en la optimización del riego suplementario[/subtitle].[/ocontrib] En: [omonog][confgrp][no]1[/no]er. [confname]Seminario Internacional de Riego en Cultivos y Pasturas. Potencial del riego extensivo en cultivos y pasturas[/confname][/confgrp]. pp. [pages]19-28[/pages][/omonog].[/ocitat]
[ocitat][no]5[/no]. [omonog][oauthor role="nd"][surname]Godagnone[/surname], [fname]RE[/fname][/oauthor]; [oauthor role="nd"][fname]H[/fname] [surname]Bertola[/surname][/oauthor] &[oauthor role="nd"][fname]M[/fname] [surname]Ancarola[/surname][/oauthor]. [date dateiso="20020000" specyear="2002"]2002[/date]. Ed. [pubname]INTA-IGM[/pubname]. Ilustraciones y cuadros[/omonog].[/ocitat]
[ocitat][no]6[/no]. [omonog][oauthor role="nd"][surname]Hudson[/surname], [fname]NW[/fname][/oauthor]. [date dateiso="19970000" specyear="1997"]1997[/date]. [title language="es"]Medición sobre el Terreno de la Erosión del Suelo y de la Escorrentía[/title]. Capítulo 3, Boletín de suelos N°68, [pubname]FAO-Organización de las Naciones Unidas para la agricultura y la alimentación[/pubname], [city]Roma[/city][/omonog].[/ocitat]
[ocitat][no]7[/no]. [ocontrib][oauthor role="nd"][surname]Jones[/surname], [fname]JW[/fname][/oauthor]; [oauthor role="nd"][fname]G.[/fname] [surname]Hoogenboom[/surname][/oauthor]; [oauthor role="nd"][fname]CH[/fname] [surname]Porter[/surname][/oauthor]; [oauthor role="nd"][fname]KJ[/fname] [surname]Boote[/surname][/oauthor]; [oauthor role="nd"][fname]WD[/fname] [surname]Batchelor[/surname][/oauthor]; [oauthor role="nd"][fname]LA[/fname] [surname]Hunt[/surname][/oauthor]; [oauthor role="nd"][fname]PW[/fname] [surname]Wilkens[/surname][/oauthor]; [oauthor role="nd"][fname]U[/fname] [surname]Singh[/surname][/oauthor]; [oauthor role="nd"][fname]AJ[/fname] [surname]Gijsman[/surname][/oauthor] & [oauthor role="nd"][fname]JT[/fname] [surname]Ritchie[/surname][/oauthor], [date dateiso="20100000" specyear="2010"]2010[/date]. [title language="en"]The DSSAT cropping system model[/title].[/ocontrib] [oiserial][sertitle]European Journal of Agronomy[/sertitle] pp. [pages]235-265[/pages][/oiserial].[/ocitat]
[ocitat][no]8[/no]. [omonog][oauthor role="nd"][surname]Linsley[/surname], [fname]R[/fname][/oauthor]. [date dateiso="19820000" specyear="1982"]1982[/date]. [title language="en"]Hydrology for Engineers[/title]. [pubname]Book McGraw-Hill[/pubname], [extent]508 pp[/extent][/omonog].[/ocitat]
[ocitat][no]9[/no]. [omonog][ocorpaut][orgname]SCS[/orgname][/ocorpaut]. [date dateiso="19720000" specyear="1972"]1972[/date]. [title language="en"]National Engineering Handbock[/title], [othinfo]Section 4, Hydrology[/othinfo], U.S. [pubname]Department of agriculture, U.S. Govermment Printing Office[/pubname], [city]Washington[/city], [state]DC[/state][/omonog].[/ocitat]
[ocitat][no]10[/no]. [omonog][oauthor role="nd"][surname]Mishra[/surname], [fname]SK[/fname][/oauthor] & [oauthor role="nd"][fname]VP[/fname] [surname]Singh[/surname][/oauthor]. [date dateiso="20030000" specyear="2003"]2003[/date]. [title language="en"]Soil conservation service curve number (SCS-CN) methodology[/title]. Vol. [volid]42[/volid], [coltitle]Water Science and Technology Library[/coltitle], ISBN [isbn]1-4020-1132-6[/isbn], [extent]513 pp[/extent][/omonog].[/ocitat]
[ocitat][no]11[/no]. [omonog][oauthor role="nd"][surname]Neter[/surname], [fname]J[/fname][/oauthor]; [oauthor role="nd"][fname]M[/fname] [surname]Kutner[/surname][/oauthor]; [oauthor role="nd"][fname]CJ[/fname] [surname]Nachtsheim[/surname][/oauthor] & [oauthor role="nd"][fname]W[/fname] [surname]Wasserman[/surname][/oauthor]. [date dateiso="19960000" specyear="1996"]1996[/date]. [title language="en"]Applied Linear Statistical Models[/title]. [edition]4ta[/edition] Edición, Editorial [pubname]WCB[/pubname]/[pubname]McGraw-Hill[/pubname], [country]Estados Unidos[/country][/omonog].[/ocitat]
[ocitat][no]12[/no]. [omonog][oauthor role="nd"][surname]Panigatti[/surname], [fname]JL[/fname][/oauthor]. [date dateiso="20100000" specyear="2010"]2010[/date]. [title language="es"]Argentina 200 años, 200 suelos[/title]. Ed. [pubname]INTA[/pubname], [city]Buenos Aires[/city], [extent]345 pp[/extent][/omonog].[/ocitat]
[ocitat][no]13[/no]. [ocontrib][oauthor role="nd"][surname]Pellat[/surname], [fname]FP[/fname][/oauthor]. [date dateiso="20090000" specyear="2009"]2009[/date]. [title language="es"]Mitos y falacias del método hidrológico del número de curva del SCS/NRCS[/title].[/ocontrib] [oiserial][sertitle]Agrociencia[/sertitle] Vol. [volid]43[/volid],N°[issueno]5 [/issueno], [country]México[/country]. Pp.[pages]521-528[/pages][/oiserial].[/ocitat]
[ocitat][no]14[/no]. [ocontrib][oauthor role="nd"][surname]Sasal[/surname], [fname]MC[/fname][/oauthor]; [oauthor role="nd"][fname]MG[/fname] [surname]Castiglioni[/surname][/oauthor] & [oauthor role="nd"][fname]MG[/fname] [surname]Wilson[/surname][/oauthor]. [date dateiso="20100000" specyear="2010"]2010[/date]. [title language="en"]Effect of crop sequences on soil properties and runoff on rainfall erosion plots under no tillage[/title].[/ocontrib] [oiserial][sertitle]Soil & Tillage Research[/sertitle] [volid]108[/volid]: [pages]24-29[/pages][/oiserial].[/ocitat]
[ocitat][no]15[/no]. [ocontrib][oauthor role="nd"][surname]Weir[/surname] [fname]Edgardo[/fname][/oauthor]. [date dateiso="20020000" specyear="2002"]2002[/date]. [title language="es"]Pérdida de suelo y agua en parcelas de escurrimiento[/title].[/ocontrib] En: [omonog][oauthor role="ed"][fname]A[/fname]. [surname]Andriulo[/surname][/oauthor] (ed), [title language="es"]Por una agricultura sin contaminantes[/title]. Proyecto de contaminación Agrícola del [pubname]INTA[/pubname], [city]Pergamino[/city], [country]Argentina[/country][/omonog][/ocitat].[/other][/back][/article]