NOTAS

Estudio fractal de la distribución de partículas y pseudopartículas en suelos de la pradera pampeana

Fractal study of the distribution of particles and pseudoparticles in soils of the pampean meadow

Pablo Raul Gelati^1*; Guillermo Oliverio Sarli¹; Luis Alberto Lozano^1-2; Roberto Raul Filgueira^1-2

¹ FCAYF UNLP
² CONICET
* Autor de contacto: prgelati@gmail.com

Recibido: 14/2/2017
Recibido con revisiones: 15/8/2018
Aceptado: 15/8/2018

RESUMEN
La geometría fractal permite describir teóricamente estructuras de diversa naturaleza. De esta se obtiene, la dimensión fractal de fragmentación (D), la cual, está relacionada con el particionamiento y escalamiento que presentan las mismas, y que ha sido empleada en la caracterización y estudio de distribución de tamaño de partículas del suelo (DTP). Se planteó aplicar el modelo fractal e investigar sobre el proceso de microestructuración en seis suelos agrícolas de la pradera pampeana con DTP contrastantes. Las DTP y las D se obtuvieron bajo dos pretratamientos, uno sin materia orgánica (SMO), máxima dispersión, y otro con materia orgánica (CMO) conservando así la microestructura. El modelo fractal aplicado a la DTP con el pretratamiento SMO, en los suelos franco limosos, alcanzó a describir en promedio el 98% de la masa analizada; en el suelo franco arenoso ajustó hasta los 50 μm, describiendo el 38% de la masa, mientas que el suelo areno franco no ajustó al modelo fractal. Con los tamaños mayores de de las arenas se obtuvieron D próximas a 3, mostrando características euclideanas, no fractales. Las DTP para el pretratamiento CMO tuvieron similar comportamiento entre los suelos evaluados, comparado con el pretratamiento SMO, disminuyeron los porcentajes de las fracciones correspondientes a los tamaños arcilla y limo; y aumentó el porcentaje del tamaño de las arenas. A estas fracciones, CMO, se las denominó "arcilla, limo y arena aparentes". Las D a partir del pretratamiento SMO fueron mayores que las obtenidas bajo el pretratamiento CMO. La disminución de la D del pretratamiento CMO, se interpretó como un engrosamiento aparente del suelo producto de la microestructuración por materia orgánica (MO). El ajuste entre los contenidos de arcillas aparentes vs MO no fue significativo (p=0,37). La fracción limo aparente vs MO, ajustó significativamente a una función exponencial negativa mientras que los contenidos de las arenas aparentes vs MO ajustaron significativamente con una función exponencial positiva. Las variaciones de MO modifican significativamente la microestructuración en los tamaños limo y arena mientras que la fracción de tamaño arcilla sería independiente del contenido de MO del suelo, en el rango analizado. En suelos templados pampeanos, con proporción de arcilla+limo próximas al 90%, la MO por microestructuración, reduce los contenidos de partículas de tamaños arcilla y limo incrementando las de tamaño arenas a valores próximos al 55% y estas modificaciones pueden interpretarse empleando el modelo fractal.

Palabras claves: Sedimentación, textura del suelo, fragmentación

ABSTRACT
Fractal geometry allows describing theoretically structures of diverse nature. From this it obtain the fractal dimension of fragmentation (D), which is related to the partitioning and scaling presented by them, and which has been used in the characterization and study of the size distribution soil particle (DTP). It was proposed to apply the fractal model and investigate the process of micro-structuring in six agricultural soils of the Pampean meadow that have contrasting DTP. The DTP and D were obtained under two pretreatments, one without organic matter (SMO), maximum dispersion, and the other with organic matter (CMO), thus preserving the microstructure. The fractal model applied to the DTP with the SMO pretreatment, in silty loam soils, was able to describe on average 98% of the mass analyzed; in sandy loam soil it adjusted to 50 μm, describing 38% of the mass, while the sandy loam soil did not adjust to the fractal model. With the larger sizes of the sands, they obtained D close to 3, showing Euclidean characteristics, not fractals. The DTP for the CMO pretreatment had similar behavior among the evaluated soils, compared to the SMO pretreatment, the percentages of the fractions corresponding to the clay and silt sizes decreased; and the percentage of the size of the sands increased. These fractions, CMO, were called "apparent clay, silt and sand". The D from the SMO pretreatment were greater than those obtained under the CMO pretreatment. The decrease of the D of the pretreatment CMO, was interpreted as an apparent thickening of the soil product of the microstructure by organic matter (OM). The fit between the contents of apparent clays vs OM was not significant (p = 0.37). The apparent silt fraction vs OM, adjusted significantly to a negative exponential function while the contents of the apparent sands vs OM adjusted significantly with a positive exponential function. The variations of OM significantly modify the microstructure in the silt and sand sizes while the fraction of clay size would be independent of the OM content of the soil, in the analyzed range. In temperate Pampas soils, with a proportion of clay + silt close to 90%, the OM by microstructure reduces the contents of clay and silt size particles, increasing the sand size to values close to 55% and these modifications can be interpreted using the model fractal.

Key words: Sedimentation, soil texture, fragmentation

INTRODUCCIÓN

La geometría fractal (Mandelbrot, 1982) ha permitido describir teóricamente estructuras que se observan en la naturaleza. Es así que las características geométricas de la distribución espacial de las raíces, las longitudes de las costas y fronteras, el fraccionamiento de las rocas y la distribución de tamaño de partículas en el suelo, entre otros, pueden ser idealizados satisfactoriamente mediante esta teoría (Korvin, 1992; Tyler & Wheatcraft, 1992; Filgueira et al., 2003, 2005; Vdovic et al., 2010; Caruso et al., 2011). Un objeto fractal está compuesto de una cantidad de estructuras similares superpuestas, visibles a cualquier nivel de detalle. Esta propiedad se conoce como autosimilitud. El material en un objeto fractal se distribuye en forma heterogénea, pero no al azar, de forma que un patrón de generación se ve idéntico, al menos en el sentido estadístico, independientemente de la amplificación con que se lo esté observando. En un fractal matemático los detalles se ven idénticos en cualquier nivel de amplificación, mientras que en un fractal natural es esperable que el nivel de repetición de la propiedad particular sea limitado a varios órdenes de magnitud, Avnir et al., (1998) han planteado dudas sobre la validez de este marco teórico, acerca del rango de aplicación de la propiedad de autosimilitud, siendo en los fractales naturales de uno o dos órdenes de magnitud.

La distribución del tamaño de partículas (DTP), es una de las características más estables en el suelo. El interés en su determinación, radica en que está relacionada con propiedades físicas y químicas como: retención hídrica, porosidad, conductividad hidráulica, capacidad de intercambio catiónico, superficie específica, compresibilidad y comportamiento térmico, susceptibilidad a la erosión y desertificación, composición química y crecimiento de las plantas, entre otras (Campbell & Shiozawa, 1992; Gelati et al., 2009; Vdovic et al., 2010). También se utiliza para la estimación de propiedades hidrológicas de suelos a través de las funciones de pedotransferencia (Pachepsky & Rawls, 2004).

En la ciencia del suelo se ha utilizado la geometría fractal para arrojar nueva luz sobre la compleja dinámica de los procesos formadores del suelo a través del estudio de las DTP (Tyler & Wheatcraft, 1992; Hyslip & Vallejo, 1997; Bittelli et al., 1999; Taguas et al., 1999; Perfect et al., 2002; Millán et al., 2003; Stanchi et al., 2006, 2008). Inicialmente, el estudio del comportamiento fractal de una distribución de partículas, se realizó en base al análisis del número de ellas (Mandelbrot, 1982; Turcotte, 1986; Tyler & Wheatcraft, 1989; Rieu & Sposito, 1991b). Tyler & Wheatcraft (1992) plantearon una forma alternativa, empleando directamente la masa de suelo, en vez del número de partículas. Esta última, es experimentalmente más precisa y directa, siendo más adecuada desde el punto de vista físico, con resultados de D menores que 3. Un valor de D mayor a 3 carece de sentido físico porque implica una probabilidad de ocurrencia mayor a uno. (Tyler & Wheatcraft, 1992). La ecuación 1 presenta el modelo utilizado por Tyler & Wheatcraft, 1992:

Donde, MT es la masa total de la distribución de las partículas, M_(r<R) es la masa parcial hasta el radio r, siendo R_Lsup es un radio límite superior de tamaño para el comportamiento fractal, c es una constante y D es la dimensión fractal de fragmentación. En el caso del experimento de sedimentación en agua para determinar la DTP, es común obtener la fracción de masa de aquellas que aún permanecen en la suspensión, es decir [M(r<R)/M_T].

Explicitando la ecuación 1 y expresándola en función de los diámetros, obtuvimos la siguiente expresión:

La nomenclatura es similar a la anterior, coincidiendo M_T, c y D. M_p es la masa parcial acumulada hasta el tamaño Ø_p (μm), Ø_m (μm) es el diámetro máximo de tamaño para el comportamiento fractal.

La distribución de tamaño de partículas o agregados, frecuentemente se las interpreta como una función acumulativa, ya sea, como el número de partículas mayores que un cierto diámetro o como la masa menor correspondiente a un determinado diámetro. Estas funciones acumulativas han sido analizadas por diversos autores como ecuaciones del tipo potencial y los exponentes interpretados como dimensiones fractales de fragmentación. Tyler & Wheatcraft, (1992), aplicando la ecuación 1, concluyeron que sólo algunos suelos dentro del triángulo textural podrían tener la DTP fractal. En este sentido, Filgueira et al., (2004), estudiaron DTP en suelos del centro oeste de la provincia de Buenos Aires que no correspondían con el modelo de distribución propuesto. Además, si bien diversos autores han encontrado que la DTP de algunos suelos puede ser caracterizada por una sola D (Turcotte, 1986; Tyler & Wheatcraft, 1992; Filgueira et al., 2006), en otros estudios se han identificado más de una escala de dominio con distintas D en el mismo suelo (Vdovic et al., 2010).

La DTP depende de los pretratamientos realizados sobre las muestras, e.g. eliminación total o parcial de agentes de agregación como materia orgánica y/o carbonato de calcio, el agregado de dispersantes químicos y la realización de dispersión física. (Gee & Bauder, 1986; Dur et al., 2004; Eshel et al., 2004; Filgueira et al., 2006, 2009; Gelati et al., 2008, 2010). Stanchi et al., (2008), propusieron relacionar la D con los procesos formadores a partir de la evaluación de la DTP en varios órdenes de suelo y analizando las sedimentaciones con diversos pretratamientos. En sus trabajos, evaluaron las DTP desde 1 hasta 2000 μm, mientras que otros autores (Bittelli et al., 1999; Filgueira et al., 2006) utilizaron el modelo fractal sólo para describir las fracciones arena y arcilla-limo por separado. El criterio empleado por Stanchi et al., (2008), fue utilizar solamente el R² resultante de los ajustes a los datos experimentales para definir si la DTP era fractal o no. Para ello, se consideró que los suelos fractales poseían un R² >0,95.

En este trabajo se hipotetizó que "la distribución de tamaño de partículas y pseudopartículas de suelos templados pampeanos sigue el modelo fractal de fragmentación y la D se modifica según el contenido de agentes estructurantes en el suelo".

Los objetivos fueron obtener para estos suelos, los parámetros fractales c y D de fragmentación a partir de las curvas de sedimentación en muestras de suelos con un pretratamiento que favorezca la máxima dispersión y otro que la minimice. Además, se planteó investigar el proceso de microestructuración en relación al contenido de materia orgánica.

MATERIALES Y MÉTODOS

Se analizaron muestras superficiales (0-15 cm) de suelos agrícolas de la región pampeana, las cuales se secaron a 40°C con circulación forzada de aire. Las mismas fueron desagregadas y tamizadas por 2 mm. A partir de las coordenadas del sitio de muestreo y los resultados de las determinaciones en laboratorio abajo descriptas, se las asoció con las series Arrecifes (Ar), Portela (Po), Bombeador (Bo), Magdalena (Md), Piedri tas (Pas) y Pirovano (Pv). Para ello se empleó el sistema Geointa (2008) y una carta de suelos de Estación Experimental Julio A Hirschhörn de la Facultad de Ciencias Agrarias y Forestales relevada por Lanfranco et al., (1970). Para caracterizar las muestras se evaluó, pH real (1:2,5, relación suelo-agua), carbono orgánico total (COT) por combustión húmeda (Walkley y Black, 1934) empleando micrométodo (Richter, 1981) y capacidad de intercambio catiónico (CIC) por el método del acetato de amonio 1 N pH 7, siguiendo los protocolos propuestos en SAMLA, (2004). Se verificó la ausencia de carbonatos con HCl.

Las sedimentaciones se hicieron según dos pretratamientos: Pretratamiento SMO (sin materia orgánica) de máxima dispersión, a partir de 20 a 30 g según la textura del suelo, se eliminó la materia orgánica con H₂O₂ y calor y se aplicó NaOH 1 N como dispersante químico y agitación rotativa con esferitas de vidrio por 24 h como dispersante físico (Gee & Bauder, 1986). Las arenas se cuantificaron con una torre de tamices (2000, 1000, 500, 250, 105, 75 y 53 μm). Para el pretratamiento de mínima dispersión, CMO (con materia orgánica) se tomó 30 a 40 g de suelo y se agregó 10 mL de alcohol etílico para humectarla y minimizar el efecto dispersivo del agua. Luego se enrasó la probeta en 1000 mL con agua destilada y las sedimentaciones se realizaron inmediatamente.

Se calcularon los tiempos empleando la ley de Stokes para obtener los diámetros aparentes de 50, 25, 10, 5 y 2 μm en las sedimentaciones, extrayendo las alícuotas con una pipeta de simple aforo de 25 mL. Todas las determinaciones se realizaron por duplicado. A partir de estos resultados se obtuvieron los datos para calcular la DTP y las clases texturales. Se denominó "Textura aparente" a la sumatoria de las fracciones correspondientes a los tamaños arena, limo y arcilla obtenidas con el pretratamiento CMO.

A partir de los datos de masa acumulada versus diámetro, empleando la ecuación potencial 2 linealizada mediante log-log, se obtuvieron los parámetros c y D para ambos pretratamientos. Se analizaron los residuos y el R² para determinar si el modelo ajusta a la DTP experimental de los suelos. Se calculó la variación de arena, limo y arcilla, en porcentaje entre pretratamientos como se indica:

(3)

ΔF(%)= variación de la fracción analizada según los pretratamientos, correspondiente a los tamaños arena, limo y arcilla.
F(CMO)= fracción analizada, obtenida según el pretratamiento CMO
F(SMO)= misma fracción analizada, obtenida con el pretratamiento SMO

Operando matemáticamente, con la ecuación 2 y empleando la identidad:

(4)

Obtuvimos las siguientes expresiones, función Iso D, con dimensión fractal constante:

(5)

Función Iso Ø_m, con diámetro máximo constante:

(6)

Donde:

M_a= masa de arcilla
M_L= masa de limo
M_A= masa de arena
Ø_a= diámetro máximo de arcillas, 2 μm
Ø_L= diámetro máximo de limos, 50 μm
Ø_m= diámetro máximo de partícula considerada 50<Ø_m<2000 μm

En el triángulo textural la gráfica de la ecuación 5, une puntos con igual D, mientras que la ecuación 6, representa puntos con igual diámetro máximo. De la ecuación 5, puede obtenerse en forma teórica la D, a partir de los contenidos de arena y arcilla del suelo. Los análisis estadísticos se realizaron empleando el software InfoStat (Di Rienzo et al., 2016).

RESULTADOS Y DISCUSIÓN

Distribución del tamaño de partículas para el pretratamiento SMO

La DTP ajustó a un modelo fractal, en los suelos Ar, Po, Bo y Md de textura franco limosa. Los coeficientes de determinación R² fueron superiores al 0,99 (Tabla 1) y la distribución de residuos aleatoria. En estos suelos, el modelo fractal alcanzó describir prácticamente la totalidad de la masa (Figura 1a). Las arenas encontradas en su mayoría correspondieron al tipo arenas muy finas y escasas de tamaño fina.

Tabla 1. SMO: pretratamiento sin materia orgánica, de máxima dispersión; CMO: pretratamiento con materia orgánica, mínima dispersión conservando la microestructura. pH real, (1:2,5) relación suelo : agua; COT carbono orgánico total (g kg^-1); CIC, capacidad de intercambio catiónico (cmol_c kg^-1); c, parámetro de la regresión; D, dimensión fractal de fragmentación. p-valor, significancia. R² Aj, coeficiente de determinación R² ajustado de la regresión.
Table 1. SMO: pretreatment without organic matter, maximum dispersion; CMO: pretreatment with organic matter, minimal dispersion conserving the microstructure. Actual pH, (1: 2.5) soil: water ratio; TOC total organic carbon (g kg- 1); CIC, cation exchange capacity (cmol_c kg^-1); c, regression parameter; D, fractal dimension of fragmentation. p-value, significance. R² Aj, coefficient of determination R² adjusted for the regression.

El diámetro promedio teórico máximo predicho por el modelo fue de 73 μm, mientras que los diámetros máximos experimentales encontrados fueron de 250 μm. La masa experimental entre 75 y 250 μm fue en promedio del 2,1% del total, y no fue incluida en el modelo. En la Figura 1a se presenta la DTP de la serie Ar como representativa de estos suelos. A las arenas comprendidas entre 105 y 250 μm se les ajustó el modelo fractal y obtuvo una D=2,991 (p=0,035), este valor de D, próximo a 3,0 es propio de cuerpos euclideanos, por lo tanto no fractales. Lo obtenido, coincide con la bibliografía en donde es mencionado que las arenas no siguen una distribución fractal (Avnir et al., 1985; Bartoli, et al., 1991; Barak., 1996).

Estos resultados pueden asociarse a trabajos pioneros realizados por Codoni, (1943), sobre la caracterización de suelos en laboratorio en la provincia de Santa Fe. Este autor proponía específicamente para la determinación de la DTP el empleo de una ecuación potencial linealizada mediante log-log. Esto tenía la ventaja que con dos datos experimentales era posible obtener los parámetros de la regresión y de esta forma la DTP del suelo. Los suelos sobre los que trabajó eran principalmente franco limosos como estos cuatro suelos aquí estudiados.

Figura 1. Relación entre la masa de partículas acumulada en función del diámetro, transformados mediante log (m%) - log (Øμm) con ambos pretratamientos. 1a). Ejemplo del suelo Ar, franco limoso; 1b) suelo Pas, franco arenoso y 1c) suelo Pv, areno franco. + SMO y o CMO, valores observados experimentalmente; con línea llena los valores predichos por el modelo fractal.
Figure 1. Relationship between the accumulated mass of particles as a function of diameter, transformed by log (m%) - log (Øμm) with both pretreatments. 1a). Example of soil Ar, silty loam; 1b) soil Pas, sandy loam and 1c) soil Pv, loamy sand. + SMO and o CMO, values observed experimentally; with full line the values predicted by the fractal model.

Los suelos de la serie Pas y Pv de texturas franco arenoso y areno franco, debieron analizarse por separado. En el suelo Pas, la DTP experimental muestra una inflexión entre los 50 y 75 μm (cuya equivalencia en Log es 1,699 y 1,875 respectivamente) y subestima sistemáticamente la fracción arena, (Figura 1b). Siguiendo el criterio planteado por Bitelli et al., (1999) y Filgueira et al., (2006), se acotó el modelo, hasta el tamaño máximo de los limos (50 μm), obteniéndose así un ajuste (R²=0,99; p<0,001) y residuos aleatorios. El modelo alcanzó a describir el 38% de la masa total. En el suelo Pv de clase textural areno franco, la DTP experimental presenta dos inflexiones (Figura 1c). Se probó ajustarlo hasta el dominio limo (50 μm) y tampoco resultó satisfactorio, la regresión no pasaba entre los valores experimentales aunque el ajuste estadístico fuera elevado (R²=0,92; p<0,01). La DTP hasta 105 μm incluyendo a las arenas muy finas, fue mejor descripta por un modelo lineal simple (R²=0,998; p<0,001) no fractal (Figura 2).

Figura 2. Suelo Pv, curva de masa acumulada en función del diámetro de partículas, ajustadas mediante un modelo lineal en el rango 2 a 105 μm.
Figure 2. Pv soil, accumulated mass curve as a function of particle diameter, adjusted by a linear model in the range 2 to 105 μm.

En los suelos Pas y Pv se analizaron las arenas en el rango de 200 a 2000 μm, obteniéndose b=0,039; (p=0,15) y b=0,052; (p=0,09) respectivamente y en ambos casos la D es próxima a 3. Obtuvimos similares resultados a otros investigadores (Avnir et al., 1985; Bartoli et al., 1991; Barak., 1996).

A partir de estos resultados se pone en evidencia que el criterio empleado por Stanchi et al., (2008), de analizar todo el rango de tierra fina y emplear el coeficiente de determinación R² como único criterio para decidir si la DTP ajusta al modelo fractal, carece de fundamento físico y el modelo poco representa la DTP del suelo, sobre todo cuando intervienen arenas en proporciones medias a elevadas.

Distribución de tamaños de partículas para el pretratamiento CMO

Los valores aparentes para cada fracción (tamaño arena, limo y arcilla) mostraron respectivamente diferencias evidentes respecto a los valores reales para cada suelo, independientemente de la clase textural. El comportamiento fue semejante en los seis suelos. Se encontró menores valores en las fracciones de tamaño arcillas y limos y mayores valores en la fracción de arenas (Figura 1 a,b,c; Tabla 2).

Tabla 2. Granulometría, con el pretratamiento SMO y granulometría aparente con el pretratamiento CMO; C.T. clase textural y C.T. ap clase textural aparente; FL, franco limoso; FA, franco arenoso; AF arenoso franco; A, arenoso.
Table 2. Granulometry, with the SMO pretreatment and apparent granulometry with the CMO pretreatment; C.T. textural class and C.T. ap apparent textural class; FL, silty loam; FA, sandy loam; AF loamy sand; A, sand.

El modelo fractal ajustó adecuadamente a la DTP de los suelos siendo el alcance hasta 50 μm. Se observó una reducción del valor de D, estos resultados coinciden con el marco teórico, donde esta reducción, puede interpretarse como un desplazamiento hacia clases más groseramente particionadas (Rieu & Sposito, 1991a; Rieu & Sposito, 1991b; Tyler SW & SW Wheatcraft, 1992; Valdez Cepeda et al., 1998) (Tabla 1, 2 y Figura 3).

Figura 3. Variación de las fracciones granulométricas para cada suelo, variación de arena, ΔA (%), variación de limo ΔL (%) y variación de arcilla Δarc (%).
Figure 3. Variation of the granulometric fractions for each soil, variation of sand, ΔA (%), variation of silt ΔL (%) and variation of clay Δarc (%).

Se encontró reducciones en el parámetro c y en los ajustes del coeficiente de determinación R²(Tabla 1)

En estos suelos, sin carbonatos ni salinidad, la diferencia entre valores reales y aparentes de cada fracción se interpretó como el resultado de la microestructuración por efecto de la MO, pasando a granulometrías mayores por incremento en la fracción de arenas aparentes y reducción de las arcillas y limos aparentes, explicitando lo reportado por Gee & Bauder, (1986).

Las D experimentales y las D teóricas obtenidas de la ecuación 5 no mostraron diferencias significativas en el pretratamiento SMO (p=0,71) ni en el pretratamiento CMO (p=0,41). Por lo tanto, podrían estimarse las D a partir de los contenidos de arena y arcilla del suelo con ambos pretratamientos empleando dicha ecuación.

La ΔArena(%) fue positiva siendo su resultado el más variable, desde 15,6 a 688%. Los suelos franco limosos, mostraron las mayores variaciones en esta fracción, debido a la mediana proporción de coloides y los menores contenidos de arena real (Figura 3). La ΔLimo (%) fue negativa mostrando un rango de variación de -27,3 a -48,5%. Las partículas de este tamaño se estructuraron por efecto de la materia orgánica y suman a la fracción de tamaño arena (Figura 3). La Δarcilla(%) también fue negativa con un rango entre -86,1 a -96,1%. La reducción respecto al valor real fue de casi un orden de magnitud (Figura 3).

Si bien el comportamiento general de las sedimentaciones con materia orgánica fue similar, no pueden analizarse juntos los comportamientos de suelos franco limosos con franco arenoso y areno franco.

Se analizaron las fracciones aparentes en función del COT para los suelos franco limosos. La regresión lineal para el contenido de arcilla aparente, arrojó una pendiente no significativa (p=0,37 y R²=0,40). Este resultado podría deberse, a que la arcilla es la fracción más reactiva y pequeñas cantidades de COT serían suficientes para reducir a los valores de arcillas aparente observados. Existiría un umbral en el contenido de COT a partir del cual su incremento no provocaría variaciones significativas en el valor de arcillas aparentes por el mecanismo de microestructuración (Figura 4).

Figura 4. Valores de arena aparente A ap(%); limo aparente, L ap(%); arcilla aparente, arc ap(%), obtenidas con CMO, en función del contenido de COT(g kg-1).
Figure 4. Apparent sand values A ap (%); apparent silt, L ap (%); apparent clay, arc ap (%), obtained with Pretreatment B (CMO), conserving the microstructure, versus the content of TOC (g kg-1).

El porcentaje de limos aparentes mostró un comportamiento potencial, significativo y negativo (p=0,004 y R²=0,99) (Figura 4). El incremento de COT, favorece la reducción de los limos aparentes. En contraposición, las arenas aparentes presentaron el mismo tipo de relación, pero positiva (p=0,014 y R²=0,96) (Figura 4).

Estas funciones potenciales estarían mostrando que el efecto microestructurante de la MO sobre las partículas elementales de tamaños limos y arenas tiende a estabilizarse con el incremento de la misma y los mayores cambios ocurrirían con los primeros aportes de MO.

En la Figura 5 se ubicaron los suelos sobre el triángulo textural según los pretratamientos a partir de los contenidos correspondientes a los tamaños arena y arcilla mientras que también se representaron las ecuaciones 5 y 6.

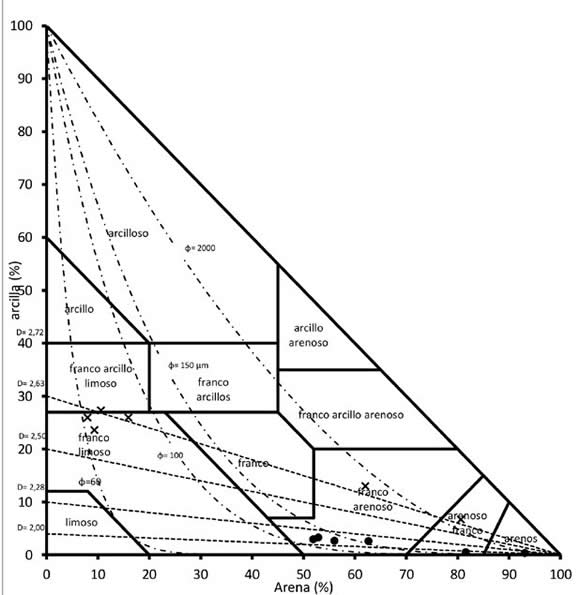
Figura 5. Triángulo textural, los suelos con el pretratamiento SMO se indican con x y los suelos con Pretratamiento CMO con ●. --- representa la función Iso D; ─ ∙ ─ representa curvas Iso Ø.
Figure 5. Textural triangle, soils with SMO pretreatment are indicated with x and soils with CMO Pretreatment with ●. --- represents the Iso D function; ─ ∙ ─ represents Iso Ø curves.

La curva de Iso Ø=2000 μm, según el modelo teórico separa el triángulo en dos áreas, a la izquierda se encuentran las combinaciones de suelos potencialmente fractales y a la derecha los no fractales. El suelo Pv, se ubicó a la derecha de esta curva coincidiendo con el marco teórico. El modelo predijo correctamente el tamaño de las arenas esperables (muy finas y finas) para los suelos franco limosos.

Las muestras con el pretratamiento CMO, quedaron próximas a la curva de Iso D= 2,0 dentro de las clases areno franco y arenoso (Figura 5).

La materia orgánica estable se encuentra significativamente correlacionada con la fracción fina del suelo y es menos sensible a las prácticas agrícolas (Galantini et al., (2008) esto puede asociarse con los resultados aquí obtenidos. El porcentaje de la fracción aparente del tamaño arcilla no variaron con el contenido de COT mientras que los tamaños mayores, limo y especialmente las arenas si son dependientes del contenido de COT. La actividad agropecuaria modifica el contenido de MO en el suelo, produciendo cambios significativos en las condiciones de microestructuración, especialmente en los tamaños de limo y arena. Podríamos asociar que las variaciones del contenido de MO en los suelos modifican directamente la textura aparente y la misma podría influir en otras propiedades físicas.

CONCLUSIONES

Los suelos con textura franco limosa presentaron una distribución de tamaño de partículas fractal. Texturas más gruesas pueden parcialmente seguir o no este modelo de fragmentación.

Las pseudopartículas modifican la dimensión fractal de fragmentación, desmejorando el ajuste al modelo propuesto.

El modelo fractal predice los tamaños máximos de partículas que podrían esperarse encontrar dentro de las diferentes clases texturales.

La D es sensible al proceso de microestructuración y a los pretratamientos, su variación con los mismos podría ser usada para construir un factor de microestructuración / dispersión.

El estado de microagregación y las proporciones de arena y limo aparente dependen del contenido de materia orgánica del suelo, en cambio la proporción de arcilla aparente no depende de este contenido.

AGRADECIMIENTOS

FCAyF-UNLP, Cátedras de Física Aplicada y Edafología

CONICET

BIBLIOGRAFÍA

1. Avnir, D; D Farin & Pfeifer. 1985. Surface geometric irregularity of particle materils: The fractal approach. J. Coll. And Interface Sci. 103:112-123.

2. Avnir, D; O Biham; D Lidar & O Malcai. 1998. Is the Geometry of Nature Fractal? Science, vol. 279 no. 5347 pp. 39-40.

3. Barak, B; C A Seybold & K Mc Sweeney. 1996. Self simitude and fractal dimension of sand grains. Soil Sci Am J. 60: 72-76.

4. Bartoli, F; R Philippy; M Doirisse; S Niquet & M Dubuit. 1991. Structure and self-similarity in silty and sandy soils: The fractal approach. J. Soil Sci. 42:167-185.

5. Bittelli, M; GS Campbell & M Flury. 1999. Characterization of particle-size distribution in soil with a fragmentation model. Soil Sci Soc Am J. 63:782–788.

6. Campbell, G & S Shiozawa. 1992. Indirect methods for estimating the hidraulic propierties of unsaturated soils. University of California, Riverside., Ch. Prediction of hydraulic propierties of soils using particle-size distribution and bulk density data, Pp. 317-328.

7. Caruso, T; EK Barto; MRK Siddiky; J Smigelski & MC Rillig. 2011. Are power laws that estimate fractal dimension a good descriptor of soil structure and its link to soil biological properties? Soil Biology & Biochemistry. 43:359- 366.

8. Di Rienzo JA; F Casanoves; MG Balzarini; L Gonzalez; M Tablada & CW Robledo, InfoStat versión 2016, Grupo InfoStat, FCA, Universidad Nacional de Córdoba, Argentina, URL http://www.infostat.com.ar

9. Dur, JC; F Elsass; V Chaplain & D Tessier. 2004. The relationship between particle size distribution by laser granulometry and image analysis by transmission electron microscopy in a soil clay fraction. Eur J Soil Sci. 55: 265-270.

10. Eshel, G; GJ Levy; U Mingelgrin & MJ Singer. 2004. Critical evaluation of the use of the laser diffraction for particle size distribution analysis. Soil Sci Soc Am J. 68: 736- 743.

11. Filgueira, RR; Ya Pachepsky & LL Fournier. 2003. Timemass scaling in soil texture analysis. Soil Sci Soc Am J. 67: 1703-1706.

12. Filgueira, RR; PR Gelati; LL Fournier & GO Sarli. 2004. ¿Es la distribución de tamaño de partículas de un suelo siempre fractal?. Actas XIX Congreso Argentino de la Ciencia del Suelo. Paraná Entre Ríos, Argentina.

13. Filgueira, RR; LL Fournier; GO Sarli & CG Soracco. 2005. Distribución de partículas y agregados de suelos: el modelo fractal. En: D. Jorajuría Reología del suelo agrícola bajo tráfico. Editorial de la Universidad de La Plata. EDULP. Pp. 21-38. ISBN 950-34-0334-0.

14. Filgueira, RR; LL Fournier; CI Cerisola; PR Gelati & MG García. 2006. Particle-size distribution in soils; a critical study of the fractal model validation. Geoderma, Volume 134, Issues 3-4, 327-334.

15. Filgueira, RR; PR Gelati; LL Fournier; GO Sarli & CG Soracco. 2009. Distribución de tamaño de partículas del suelo; su estudio con un modelo fractal. XVIII Congreso Latinoamericano de la Ciencia del Suelo. Costa Rica.

16. Galantini, JA & L Suñer. 2008. Las fracciones orgánicas del suelo: análisis en suelos de la Argentina. Agriscientia. Vol XXV (1): 41-55.

17. Gee, GW & JW Bauder. 1986. Particle size analysis. Methods of soil analysis, part 1. Physical and minerological methods. Agronomy Monograph Nº 9. Second Edition. Pp. 383-411.

18. Gelati, PR; GO Sarli; LA Lozano & RR Filgueira. 2008. Arcilla: tiempos necesarios para estimar su contenido con hidrómetro según pretratamientos. XXI Congreso Argentino de la Ciencia del Suelo. Potrero de los Funes, San Luis. Argentina

19. Gelati, PR; GO Sarli; CG Soracco; LA Lozano & RR Filgueira. 2009. Influencia de la materia orgánica en la superficie específica de un Argiudol típico. Revista de la Facultad de Ciencias Agrarias, Universidad Nacional de Cuyo. Tomo XLI. N°2. ISSN 0370-4661

20. Gelati, PR; GO Sarli; LA Lozano; CG Soracco & RR Filgueira. 2010. Microagregación: análisis mediante curvas de sedimentación, XXII Congreso Argentino de la Ciencia del Suelo. Rosario, Santa Fé, Argentina.

21. GeoINTA. © Copyright 2008. INTA. Buenos Aires, Argentina. Disponible en: http://geointa.inta.gov.ar/.

22. Hyslip, J & L Vallejo. 1997. Fractal analysis of the roughness and size distribution of granular materials. Engineering Geology 48, 231-244.

23. Korvin, G. 1992. Fractal Methods in the Earth Sciences. Elsevier, Amsterdam. 191 p.

24. Lanfranco, JW & R Carrizo. 1970. Carta de suelos de la estación experimental Central Julio Hirschhörn de la FCAyF/ UNLP. Inédito.

25. Mandelbrot, B. 1982. The fractal geometry of nature. W.h. Freeman and Company. New York.

26. Millán, H; M Gonzalez-Posada; M Aguilar; J Domínguez & L Céspedes. 2003. On the fractal scaling of soil data. Particle size distributions. Geoderma 117, 117-128.

27. Pachepsky Ya & JM Rawls. 2004. Development of Pedotransfer Functions in Soil Hydrology. Development in Soil Science (Vol 30). Amsterdam. The Netherlands. 504 p.

28. Perfect, E; M Díaz Zorita & J Grove. 2002. A prefractal model for predicting soil fragment size distributions. Soil and Tillage Research 36:1-20.

29. Rieu, M & Sposito. 1991a. Fractal fragmentation, soil porosity, and soil water properties: I. Theory. Soil Sci Soc Am J. 55:1231-1238.

30. Rieu, M & Sposito. 1991b. Fractal fragmentation, soil porosity, and soil water properties: II. Applications. Soil Sci Soc Am J. 55:1239-1244.

31. SAMLA. 2004. Secretaría de Agricultura, Ganadería, Pesca y Alimentación de la Nación Argentina. Dirección de Producción Agrícola. Sistema de Apoyo Metodológico a los Laboratorios de Análisis de Suelos Agua, Vegetales y Enmiendas Orgánicas.

32. Stanchi, S; E Bonifacio; E Zanini & Ya Pachepsky. 2006. Presence and prediction of fractal behaviour in particle-size distributions as affected by the sample pretreatment and soil properties. Soil Sci. 171 (4): 283-292.

33. Stanchi, S; E Bonifacio & E Zanini. 2008. Mass-size fractal dimension of primary and aggregate particles and soil profile development. Soil Sci. 173 (2), 87-95.

34. Taguas, F; M Martín & E Perfect. 1999. Simulation and testing of self-similar estructures for soil particle size distributions using iterated function systems. Geoderma. 88: 191-203.

35. Turcotte, D L. 1986. Fractals and fragmentation. JGR. Vol. 91. No. B2. Pp. 1921-1926.

36. Tyler SW & SW Wheatcraft. 1989. Application of fractal mathematics to soils water retention estimation. Soil Sci Soc Am. J. 5: 987- 996.

37. Tyler SW & SW Wheatcraft.1992. Fractal scaling of soil particle- size distributions: analysis and limitations. Soil Sci. Soc. Am. J. 56, 362–369.

38. Valdez Cepeda, R D & E Olivares-Sáenz. 1998. Geometría fractal en la ciencia del suelo. Terra, 16(3) 277-288.

39. Vdovic, N; J Obhodas & K Pikelj. 2010.Resvisiting the particle- size distribution of soils: comparison of different methods and simple pre-treatments. Eur J Soil Sci. 61, 854-864.